洛伦兹吸引力

这是使用mplot3d在3维空间中绘制Edward Lorenz 1963年的“确定性非周期流”的示例。

注意：因为这是一个简单的非线性ODE，使用SciPy的ode求解器会更容易完成，但这种方法仅取决于NumPy。

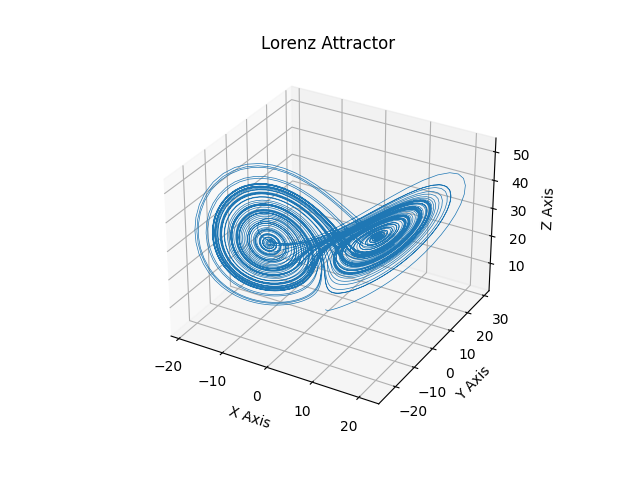
洛伦兹吸引力示例

  1. import numpy as np
  2. import matplotlib.pyplot as plt
  3. # This import registers the 3D projection, but is otherwise unused.
  4. from mpl_toolkits.mplot3d import Axes3D  # noqa: F401 unused import
  7. def lorenz(x, y, z, s=10, r=28, b=2.667):
  8.     '''
  9.     Given:
  10.        x, y, z: a point of interest in three dimensional space
  11.        s, r, b: parameters defining the lorenz attractor
  12.     Returns:
  13.        x_dot, y_dot, z_dot: values of the lorenz attractor's partial
  14.            derivatives at the point x, y, z
  15.     '''
  16.     x_dot = s*(y - x)
  17.     y_dot = r*x - y - x*z
  18.     z_dot = x*y - b*z
  19.     return x_dot, y_dot, z_dot
  22. dt = 0.01
  23. num_steps = 10000
  25. # Need one more for the initial values
  26. xs = np.empty((num_steps + 1,))
  27. ys = np.empty((num_steps + 1,))
  28. zs = np.empty((num_steps + 1,))
  30. # Set initial values
  31. xs[0], ys[0], zs[0] = (0., 1., 1.05)
  33. # Step through "time", calculating the partial derivatives at the current point
  34. # and using them to estimate the next point
  35. for i in range(num_steps):
  36.     x_dot, y_dot, z_dot = lorenz(xs[i], ys[i], zs[i])
  37.     xs[i + 1] = xs[i] + (x_dot * dt)
  38.     ys[i + 1] = ys[i] + (y_dot * dt)
  39.     zs[i + 1] = zs[i] + (z_dot * dt)
  42. # Plot
  43. fig = plt.figure()
  44. ax = fig.gca(projection='3d')
  46. ax.plot(xs, ys, zs, lw=0.5)
  47. ax.set_xlabel("X Axis")
  48. ax.set_ylabel("Y Axis")
  49. ax.set_zlabel("Z Axis")
  50. ax.set_title("Lorenz Attractor")
  52. plt.show()

下载这个示例