递归与回溯

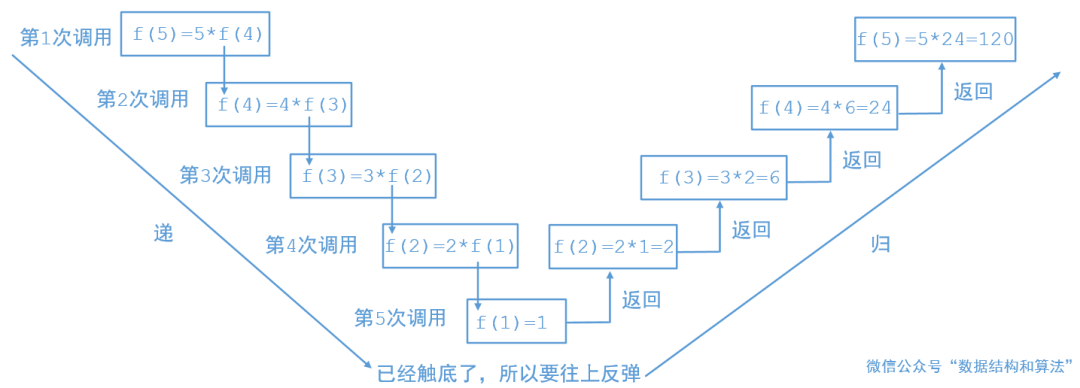
0. 重要思想

递归的目的是把一个大的问题细分为更小的子问题，我们只需要知道递归函数的功能即可，不要把递归一层一层的拆开来想，如果同时调用多次的话这样你很可能会陷入循环而出不来。
一定要明白递归函数中每个参数的含义，这样在逻辑处理和函数调用的时候才能得心应手。

1. 啥是递归

递归，就是在运行的过程中调用自己。

2. 构成递归需具备的条件：

1. 子问题必须与原始问题为同样的问题，且求解更为简单； 递归调用
   2. 不能无限制地调用本身，须有个出口，化简为非递归状况处理。 终止条件

3. 递归模板

void recur(param0)
{
    if (终止条件)
        return;
    recur(param1);    //调用自己
}

void recur(param0)
{
    if (终止条件)
        return;
    一些逻辑运算;
    recur(param1);
    一些逻辑运算;
    recur(param2);
        ...
    一些逻辑运算;
    recur(paramn);
    一些逻辑运算;
}

4. 示例分析（c语言）

1. 阶乘

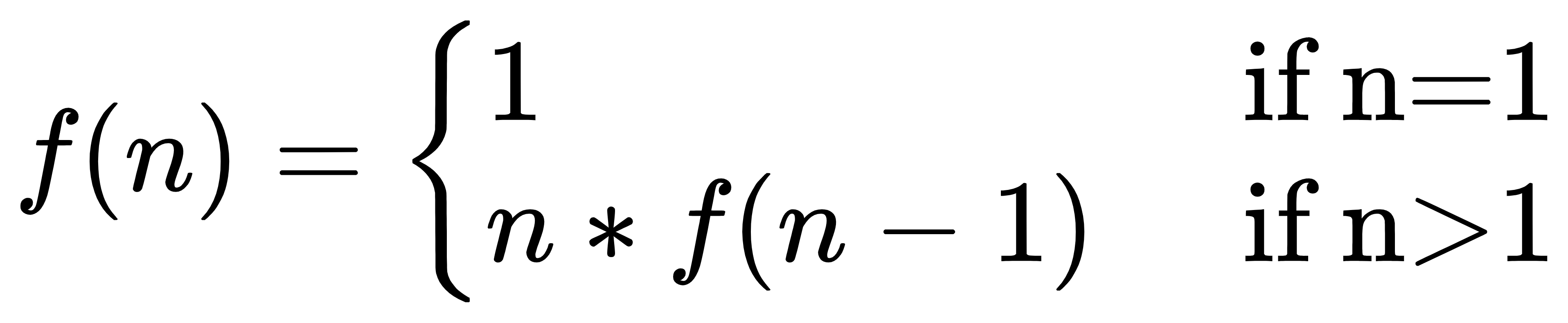
int recur(int n)
{
     if (n == 1)
        return 1;
    return n * recur(n-1);
}

2. 斐波那契数列

比阶乘复杂的地方在于递归调用在一个函数中发生了两次。
我们只需要关心函数的执行结果，而不要深究函数如何执行。
所以关键就在于对参数的理解，传进去的参数是值传递还是指针传递。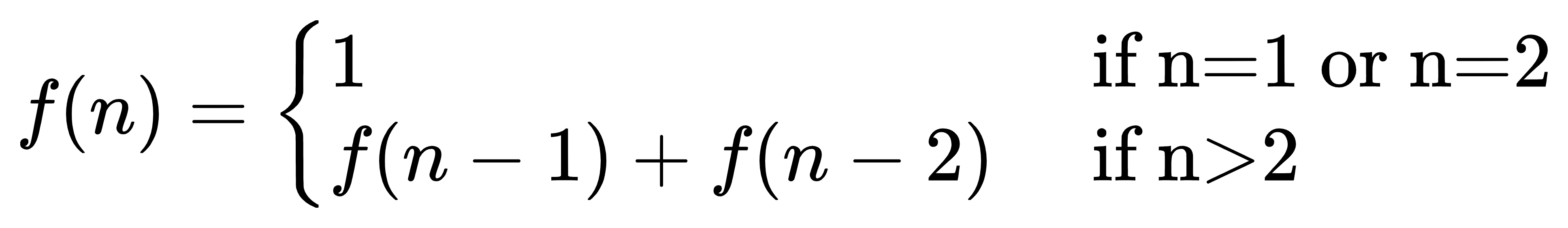

int fibonacci(int n)
{
     if (n == 1 || n == 2)
        return 1;
    return fibonacci(n - 1) + fibonacci(n - 2);
}

3. Hannoi

与之前不同的是有了更为复杂的逻辑处理语句。

汉诺塔的原理这里简单提一下，就是有3根柱子A，B，C。A柱子上由上至下依次由小至大排列的圆盘。把A柱子上的圆盘借B柱子全部移动到C柱子上，并且移动的过程始终是小的圆盘在上，大的在下。我们还是用递归的方式来解这道题，先来定义一个函数

void hanoi(int n, char A, char B, char C)
//表示的是把n个圆盘从A借助B成功的移动到C。

如何执行递归调用：
类似与把一个大象放进冰箱需要几步
1，先把n-1个圆盘从A借助C成功的移动到B（打开冰箱）
2，然后再把第n个圆盘从A移动到C（把大象塞进去）
3，最后再把n-1个圆盘从B借助A成功的移动到C。（关上冰箱）

用代码表示就是：

hannoi(n-1, 'A', 'C', 'B');
printf("从%c移动到%c\n", A, C);
hannoi(n-1, 'B', 'A', 'C');

整个代码如下：

void hannoi(int n, char a, char b, char c)
{
    if (n == 1)
    {
        printf("从%c移动到%c\n", a, c);    
        return;
    }
    hannoi(n-1, a, c, b);
    printf("从%c移动到%c\n", a, c);
    hannoi(n-1, b, a, c);
}

4. 二叉树的遍历

复习下模板

void recur(param0)
{
     if (终止条件)
    {
        逻辑处理(如果有的话);
        return;
    }
    逻辑处理(如果有的话);
    递归调用(必有);
}

先序遍历
根—>左—>右

void preOrderTraverse(struct Tree *root)
{
     if (root == NULL)
        return;
    printf("%d\n", root->data);
    preOrderTraverse(root->left);
    preOrderTraverse(root->right);
}

中序遍历
左—>根—>右

void inOrderTraverse(struct Tree *root)
{
     if (root == NULL)
        return;
    preOrderTraverse(root->left);
    printf("%d\n", root->data);
    preOrderTraverse(root->right);
}

后序遍历
左—>右—>根

void lastOrderTraverse(struct Tree *root)
{
     if (root == NULL)
        return;
    preOrderTraverse(root->left);
    preOrderTraverse(root->right);
    printf("%d\n", root->data);
}

5. 链表的逆序打印

void printReverse(struct List *root)
{
     if (root == NULL)
        return;
    printReverse(root->next);
    printf("%d\n", root->data);
}

5. 分支污染问题（Java示例）

一切乱象的根源。
通过上面的分析，我们对递归有了更深一层的认识。但总觉得还少了点什么，其实递归我们还可以通过另一种方式来认识他，就是n叉树。
在递归中如果只调用自己一次，我们可以把它想象为是一棵一叉树（摘抄见文末，我们可以认为只有一个子节点的树）；
如果调用自己2次，我们可以把它想象为一棵二叉树；
如果调用自己n次，我们可以把它想象为一棵n叉树……。
就像下面这样，当到达叶子节点的时候开始往回反弹。
每一层都是在同一个函数中。

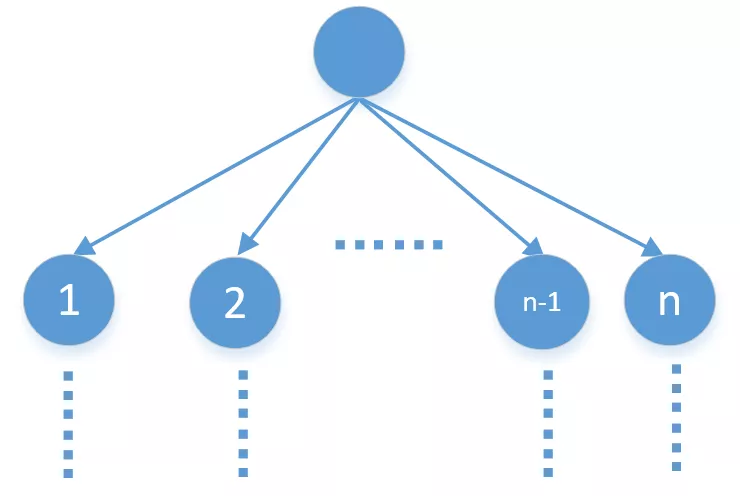
递归的时候如果处理不当可能会出现分支污染导致结果错误。为什么会出现这种情况？
因为除了基本类型是值传递以外，其他类型基本上很多都是引用传递。
看一下上面的图，比如我开始调用的时候传入一个list对象，在调用第一个分支之后list中的数据修改了，那么后面的所有分支都能感知到，实际上也就是对后面的分支造成了污染。
我们先来看一个例子吧
给定一个数组nums=[2，3，5]和一个固定的值target=8。找出数组sums中所有可以使数字和为target的组合。先来画个图看一下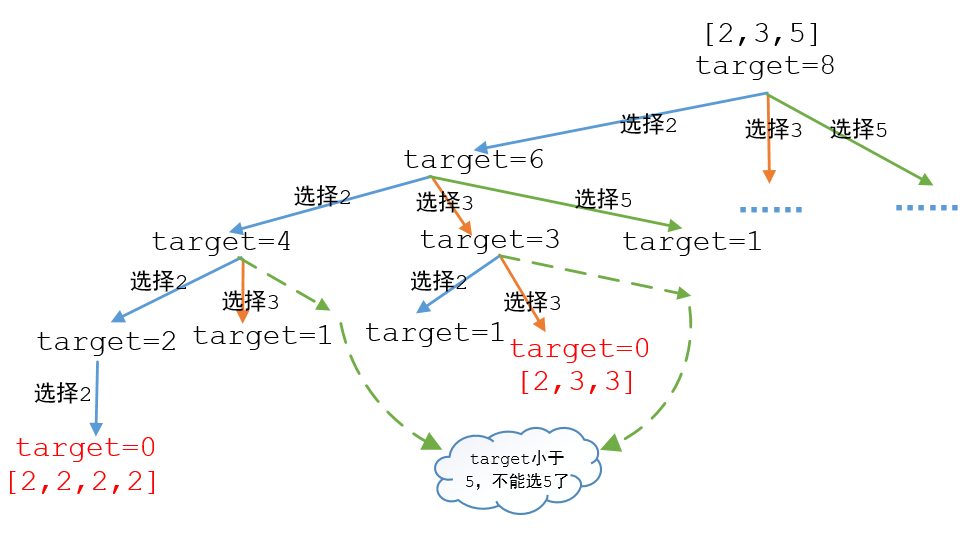

图中红色的表示的是选择成功的组合，这里只画了选择2的分支，由于图太大，所以选择3和选择5的分支没画。再仔细一看这不就是一棵3叉树吗，OK，我们来使用递归的方式，先来看一下函数的定义：

private void combinationSum(List<Integer> cur, int sums[], int target) {
}

在把递归的模板拿出来

private void combinationSum(List<Integer> cur, int sums[], int target) {2    if (终止条件) {
        return;
    }
    //逻辑处理
    //因为是3叉树，所以这里要调用3次
    //递归调用
    //递归调用
    //递归调用
    //逻辑处理
}

这种解法灵活性不是很高，如果nums的长度是3，我们3次递归调用，如果nums的长度是n，那么我们就要n次调用……。但是我们事先是不知道调用几次的。所以我们可以直接写成for循环的形式，也就是下面这样

private void combinationSum(List<Integer> cur, int sums[], int target) {
    //终止条件必须要有
    if (终止条件) {
        return;
    }
    //逻辑处理(可有可无，是情况而定)
    for (int i = 0; i < sums.length; i++) {
        //逻辑处理(可有可无，是情况而定)
        //递归调用(递归调用必须要有)
        //逻辑处理(可有可无，是情况而定)
    }
    //逻辑处理(可有可无，是情况而定)
}

下面我们再来一步一步看
1，终止条件是什么？
当target等于0的时候，说明我们找到了一组组合，我们就把他打印出来，所以终止条件很容易写，代码如下:

   if (target == 0) {
        System.out.println(Arrays.toString(cur.toArray()));
        return;
    }

2，逻辑处理和递归调用
我们一个个往下选的时候如果要选的值比target大，我们就不要选了，如果不比target大，就把他加入到list中，表示我们选了他，如果选了他之后在递归调用的时候target值就要减去选择的值，代码如下:

        //逻辑处理
        //如果当前值大于target我们就不要选了
        if (target < sums[i])
            continue;
        //否则我们就把他加入到集合中
        cur.add(sums[i]);
        //递归调用
        combinationSum(cur, sums, target - sums[i]);

终止条件和递归调用都已经写出来了，感觉代码是不是很简单，我们再来把它组合起来看下完整代码:

private void combinationSum(List<Integer> cur, int sums[], int target) {
    //终止条件必须要有
    if (target == 0) {
        System.out.println(Arrays.toString(cur.toArray()));
        return;
    }
    for (int i = 0; i < sums.length; i++) {
        //逻辑处理
        //如果当前值大于target我们就不要选了
       if (target < sums[i])
            continue;
        //否则我们就把他加入到集合中
        cur.add(sums[i]);
        //递归调用
        combinationSum(cur, sums, target - sums[i]);
    }

我们还用上面的数据打印测试一下:

public static void main(String[] args) {
    new Recursion().combinationSum(new ArrayList<>(), new int[]{2, 3, 5}, 8);
}

结果如下：

是不是很意外，我们思路并没有出错，结果为什么不对呢，其实这就是典型的分支污染，我们再来看一下图，当我们选择2的时候是一个分支，当我们选择3的时候又是另外一个分支，这两个分支的数据应该是互不干涉的，（即两个不同的函数调用）但实际上当我们沿着选择2的分支走下去的时候list中会携带选择2的那个分支的数据，当我们再选择3的那个分支的时候这些数据还依然存在list中，所以对选择3的那个分支造成了污染。有一种解决方式就是每个分支都创建一个新的list，也就是下面这样，这样任何一个分支的修改都不会影响到其他分支。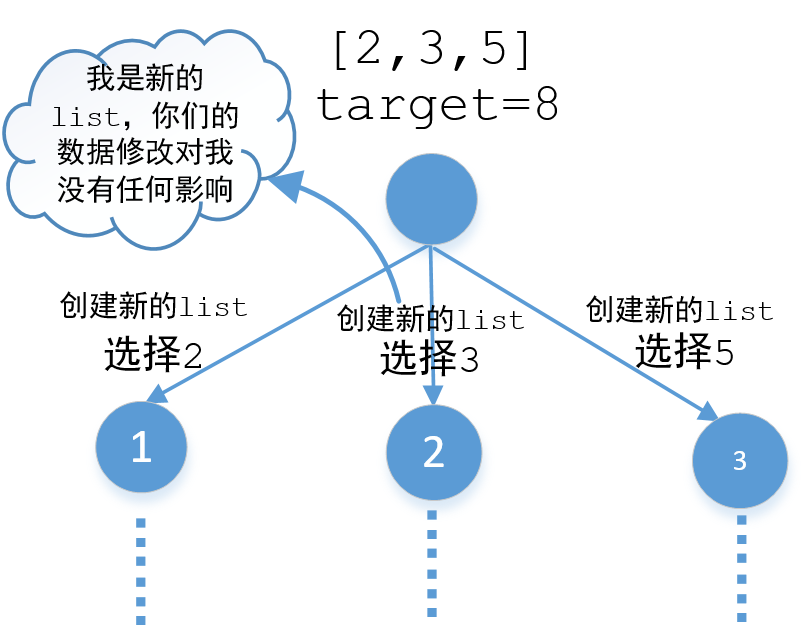

public static void combinationSum(List<Integer> cur, int sums[], int target) {
        //终止条件必须要有
        if (target == 0) {
            System.out.println(Arrays.toString(cur.toArray()));
            return;
        }
        for (int i = 0; i < sums.length; i++) {
            //逻辑处理
            //如果当前值大于target我们就不要选了
            if (target < sums[i])
                continue;
            //否则我们就把他加入到集合中
            List<Integer> list = new ArrayList<>(cur);
            list.add(sums[i]);
            //递归调用
            combinationSum(list, sums, target - sums[i]);
        }
}

我们看到第13行是重新创建了一个list。再来打印一下看下结果，结果完全正确，每一组数据的和都是8.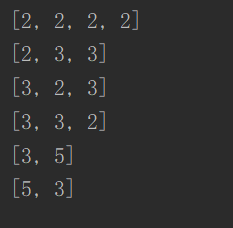
:
上面我们每一个分支都创建了一个新的list，所以任何分支修改都只会对当前分支有影响，不会影响到其他分支，也算是一种解决方式。但每次都重新创建数据，运行效率很差。

我们知道当执行完分支1的时候，list中会携带分支1的数据，当执行分支2的时候，实际上我们是不需要分支1的数据的，所以有一种方式就是从分支1执行到分支2的时候要把分支1的数据给删除，这就是大家经常提到的回溯算法，我们来看下:

private void combinationSum(List<Integer> cur, int sums[], int target) {
    //终止条件必须要有
    if (target == 0) {
        System.out.println(Arrays.toString(cur.toArray()));
        return;
    }
    for (int i = 0; i < sums.length; i++) {
        //逻辑处理
        //如果当前值大于target我们就不要选了
        if (target < sums[i])
            continue;
        //把数据sums[i]加入到集合中，然后参与下一轮的递归
        cur.add(sums[i]);
        //递归调用
        combinationSum(cur, sums, target - sums[i]);
        //sums[i]这个数据你用完了吧，我要把它删了
        cur.remove(cur.size() - 1);
    }
}

打印结果也是完全正确的。

递归分支污染对结果的影响

分支污染一般会对结果造成致命错误，但也不是绝对的，我们再来看个例子。生成一个2^n长的数组，数组的值从0到(2^n)-1，比如n是3，那么要生成：

[0, 0, 0]
[0, 0, 1]
[0, 1, 0]
[0, 1, 1]
[1, 0, 0]
[1, 0, 1]
[1, 1, 0]
[1, 1, 1]

我们先来画个图看一下：

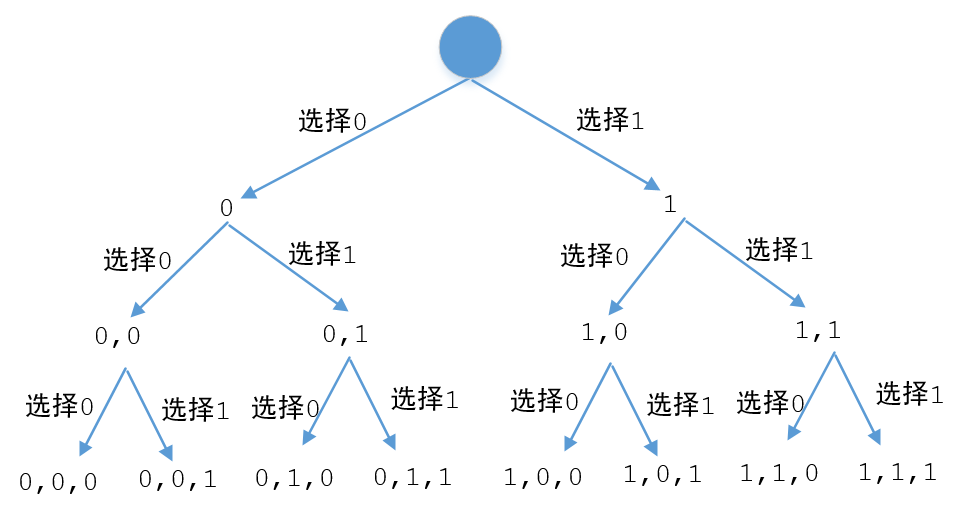
这不就是个二叉树吗，对于递归前面已经讲的很多了，我们来直接看代码

private void binary(int[] array, int index) {
     if (index == array.length) {
         System.out.println(Arrays.toString(array));
     } else {
         int temp = array[index];
         array[index] = 0;
         binary(array, index + 1);
         array[index] = 1;
         binary(array, index + 1);
        array[index] = temp;
    }
}

上面代码很好理解，首先是终止条件，然后是递归调用，在调用之前会把array[index]的值保存下来，最后再还原。我们来测试一下

• 
  

  new Recursion().binary(new int[]{0, 0, 0}, 0);

  看下打印结果

结果完全正确，我们再来改一下代码

private void binary(int[] array, int index) {
    if (index == array.length) {
        System.out.println(Arrays.toString(array));
    } else {
        array[index] = 0;
        binary(array, index + 1);
        array[index] = 1;
        binary(array, index + 1);
    }
}

再来看一下打印结果

和上面结果一模一样，开始的时候我们没有把array[index]的值保存下来，最后也没有对他进行复原，但结果丝毫不差。原因就在上面代码第5行array[index]=0，这是因为，上一分支执行的时候即使对array[index]造成了污染，在下一分支又会对他进行重新修改。即使你把它改为任何数字也都不会影响到最终结果。

6. 总结

递归核心

• 子问题与原问题求解方法一致—->递归调用
• 当问题缩小至一定规模时可以退出递归—>结束条件
• 当然想要写好一个递归函数肯定少不了逻辑处理，不同的逻辑处理就会造就前序，中序，后序这么多的差别

注意事项
一定要清楚参数是干什么的，是值传递还是指针传递，如果没搞清楚，稀里糊涂的话就会造成严重的后果！

参考：

什么是递归，通过这篇文章，让你彻底搞懂递归