🏆 第 304 场力扣周赛

最后一题急了，冷静下来想想其实没那么麻烦

6132. 使数组中所有元素都等于零

给你一个非负整数数组 nums 。在一步操作中，你必须：

• 选出一个正整数 x ，x 需要小于或等于 nums 中 最小 的 非零 元素。
• nums 中的每个正整数都减去 x。

返回使 nums 中所有元素都等于_ _0 需要的 最少 操作数。

示例 1：
输入：nums = [1,5,0,3,5] 输出：3 解释： 第一步操作：选出 x = 1 ，之后 nums = [0,4,0,2,4] 。 第二步操作：选出 x = 2 ，之后 nums = [0,2,0,0,2] 。 第三步操作：选出 x = 2 ，之后 nums = [0,0,0,0,0] 。
示例 2：
输入：nums = [0] 输出：0 解释：nums 中的每个元素都已经是 0 ，所以不需要执行任何操作。

提示：

• 1 <= nums.length <= 100
• 0 <= nums[i] <= 100

思路：
找除0外不同数的个数

class Solution {
    public int minimumOperations(int[] nums) {
        // Arrays.sort(nums);
        Set<Integer> set = new HashSet<>();
        for (int x : nums) {
            if (x == 0) continue;
            set.add(x);
        }
        return set.size();
    }
}

6133. 分组的最大数量

给你一个正整数数组 grades ，表示大学中一些学生的成绩。你打算将 所有 学生分为一些 有序 的非空分组，其中分组间的顺序满足以下全部条件：

• 第 i 个分组中的学生总成绩 小于 第 (i + 1) 个分组中的学生总成绩，对所有组均成立（除了最后一组）。
• 第 i 个分组中的学生总数 小于 第 (i + 1) 个分组中的学生总数，对所有组均成立（除了最后一组）。

返回可以形成的 最大 组数。

示例 1：
输入：grades = [10,6,12,7,3,5] 输出：3 解释：下面是形成 3 个分组的一种可行方法： - 第 1 个分组的学生成绩为 grades = [12] ，总成绩：12 ，学生数：1 - 第 2 个分组的学生成绩为 grades = [6,7] ，总成绩：6 + 7 = 13 ，学生数：2 - 第 3 个分组的学生成绩为 grades = [10,3,5] ，总成绩：10 + 3 + 5 = 18 ，学生数：3 可以证明无法形成超过 3 个分组。
示例 2：
输入：grades = [8,8] 输出：1 解释：只能形成 1 个分组，因为如果要形成 2 个分组的话，会导致每个分组中的学生数目相等。

提示：

• 1 <= grades.length <= 105
• 1 <= grades[i] <= 105

思路：
贪心，排序后从小到大，每组人数递增

class Solution {
    public int maximumGroups(int[] grades) {
        Arrays.sort(grades);
        int c = 1, s = 0;
        while (s + c <= grades.length) {
            s += c;
            c++;
        }
        return c - 1;
    }
}

6134. 找到离给定两个节点最近的节点

显示英文描述
我的提交返回竞赛

• 通过的用户数2835
• 尝试过的用户数4068
• 用户总通过次数2935
• 用户总提交次数12895
• 题目难度Medium

给你一个 n 个节点的 有向图 ，节点编号为 0 到 n - 1 ，每个节点 至多 有一条出边。
有向图用大小为 n 下标从 0 开始的数组 edges 表示，表示节点 i 有一条有向边指向 edges[i] 。如果节点 i 没有出边，那么 edges[i] == -1 。
同时给你两个节点 node1 和 node2 。
请你返回一个从 node1 和 node2 都能到达节点的编号，使节点 node1 和节点 node2 到这个节点的距离 较大值最小化。如果有多个答案，请返回 最小 的节点编号。如果答案不存在，返回 -1 。
注意 edges 可能包含环。

示例 1：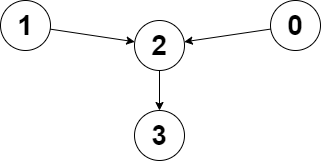

输入：edges = [2,2,3,-1], node1 = 0, node2 = 1 输出：2 解释：从节点 0 到节点 2 的距离为 1 ，从节点 1 到节点 2 的距离为 1 。 两个距离的较大值为 1 。我们无法得到一个比 1 更小的较大值，所以我们返回节点 2 。
示例 2：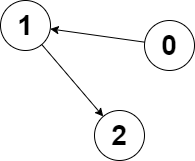

输入：edges = [1,2,-1], node1 = 0, node2 = 2 输出：2 解释：节点 0 到节点 2 的距离为 2 ，节点 2 到它自己的距离为 0 。 两个距离的较大值为 2 。我们无法得到一个比 2 更小的较大值，所以我们返回节点 2 。

提示：

• n == edges.length
• 2 <= n <= 105
• -1 <= edges[i] < n
• edges[i] != i
• 0 <= node1, node2 < n

思路：
比赛的时候用的bfs求两次最短路
其实每个点到其余所有点的路径都是唯一的，直接对着原数组遍历求就行

// 赛时代码
class Solution {
    int N = 100010;
    int[] h = new int[N], e = new int[N], ne = new int[N];
    int[] d1 = new int[N], d2 = new int[N];
    int idx, n;
    public int closestMeetingNode(int[] edges, int node1, int node2) {
        n = edges.length;
        Arrays.fill(h, -1);
        for (int i = 0; i < n; i++) {
            if (edges[i] == -1) continue;
            add(i, edges[i]);
        }
        dijk(node1, d1);
        dijk(node2, d2);
        int max = 0x3f3f3f3f, node = n;
        for (int i = 0; i < n; i++) {
            if (d1[i] == 0x3f3f3f3f || d2[i] == 0x3f3f3f3f)
                continue;
            int v = Math.max(d1[i], d2[i]);
            if (v < max) {
                max = v;
                node = i;
            }
        }
        return max == 0x3f3f3f3f ? -1 : node;
    }
    void dijk(int s, int[] d) {
        Arrays.fill(d, 0x3f3f3f3f);
        Queue<Integer> q = new LinkedList<>();
        q.offer(s);
        d[s] = 0;
        int cnt = 0;
        while (!q.isEmpty()) {
            cnt++;
            int size = q.size();
            while (size-- > 0) {
                int u = q.poll();
                for (int i = h[u]; i != -1; i = ne[i]) {
                    int j = e[i];
                    if (d[j] > cnt) {
                        d[j] = cnt;
                        q.offer(j);
                    }
                }
            }
        }
    }
    void add(int a, int b) {
        e[idx] = b;
        ne[idx] = h[a];
        h[a] = idx++;
    }
}

class Solution {
    public int closestMeetingNode(int[] e, int node1, int node2) {
        int n = e.length;
        int[] d1 = new int[n], d2 = new int[n];
        Arrays.fill(d1, 0x3f3f3f3f);
        Arrays.fill(d2, 0x3f3f3f3f);
        d1[node1] = 0;
        for (int i = node1; i >= 0; i = e[i]) {
            int j = e[i];
            if (j == -1) break;
            if (d1[j] != 0x3f3f3f3f) break;
            d1[j] = d1[i] + 1;
        }
        d2[node2] = 0;
        for (int i = node2; i >= 0; i = e[i]) {
            int j = e[i];
            if (j == -1) break;
            if (d2[j] != 0x3f3f3f3f) break;
            d2[j] = d2[i] + 1;
        }
        int max = 0x3f3f3f3f, node = -1;
        for (int i = 0; i < n; i++) {
            int v = Math.max(d1[i], d2[i]);
            if (v < max) {
                max = v;
                node = i;
            }
        }
        return node;
    }
}

6135. 图中的最长环

给你一个 n 个节点的 有向图 ，节点编号为 0 到 n - 1 ，其中每个节点 至多 有一条出边。
图用一个大小为 n 下标从 0 开始的数组 edges 表示，节点 i 到节点 edges[i] 之间有一条有向边。如果节点 i 没有出边，那么 edges[i] == -1 。
请你返回图中的 最长 环，如果没有任何环，请返回 -1 。
一个环指的是起点和终点是 同一个 节点的路径。

示例 1：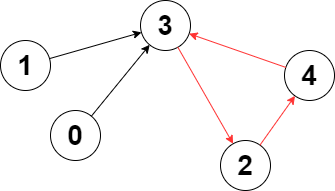

输入：edges = [3,3,4,2,3] 输出去：3 解释：图中的最长环是：2 -> 4 -> 3 -> 2 。 这个环的长度为 3 ，所以返回 3 。
示例 2：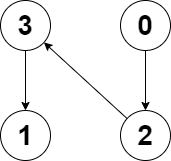

输入：edges = [2,-1,3,1] 输出：-1 解释：图中没有任何环。

提示：

• n == edges.length
• 2 <= n <= 105
• -1 <= edges[i] < n
• edges[i] != i

思路：
遍历找环 + 时间计数器

class Solution {
    public int longestCycle(int[] e) {
        int n = e.length;
        int[] time = new int[n];
        int p = 1;
        int max = -1;
        for (int i = 0; i < n; i++) {
            if (time[i] > 0) continue;
            int j = i, start = p;
            while (j != -1 && time[j] == 0) {
                time[j] = p++;
                j = e[j];
            }
            if (j != -1 && time[j] >= start)
                max = Math.max(max, p - time[j]);
        }
        return max;
    }
}
// 优化空间写法
class Solution {
    public int longestCycle(int[] e) {
        int p = 100000, base = 0xfffff;
        int max = -1;
        for (int i = 0; i < e.length; i++) {
            int j = i, c = 0;
            while (e[j] >= 0 && e[j] < e.length) {
                c++;
                int t = e[j];
                e[j] = hash(p, c);
                j = t;
            }
            if ((e[j] & base) == p) max = Math.max(max, c - (e[j] >> 20) + 1);
            p++;
        }
        return max;
    }
    int hash(int p, int c) {
        return (c << 20) + p;
    }
}