1931. 用三种不同颜色为网格涂色

给你两个整数 m 和 n 。构造一个 m x n 的网格,其中每个单元格最开始是白色。请你用 红、绿、蓝 三种颜色为每个单元格涂色。所有单元格都需要被涂色。
涂色方案需要满足:不存在相邻两个单元格颜色相同的情况 。返回网格涂色的方法数。因为答案可能非常大, 返回 对 109 + 7 取余 的结果。
示例 1:
输入:m = 1, n = 1 输出:3 解释:如上图所示,存在三种可能的涂色方案。 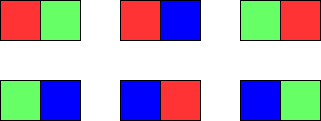
示例 2:
输入:m = 1, n = 2 输出:6 解释:如上图所示,存在六种可能的涂色方案。
示例 3:
输入:m = 5, n = 5 输出:580986
提示:
1 <= n <= 51 <= m <= 1000
思路:
对于每个方块,如果每次仅考虑一个,不仅要考虑左边与它相邻的,还得考虑上边与它相邻的,问题无法处理,因为我们不知道这两个相邻块的每种颜色对应的总取值的个数。
所以得将问题转换成处理一个相邻块,也就是说,需要提前处理好一整行的取色情况。
- 观察数据范围,选择
n作为一整行来处理,总情况为[0, 3n)种,预处理每种情况,将其中相邻块有重复颜色的情况去掉。经过运行发现当n取5时最多只有48种情况。 - 因此可以用
O(K2) <= 482的方式继续预处理相邻行的取值情况。 - 预处理结束,进行DP。
状态表示:f[i][j]表示当第i行填色情况为j时前i行的总取值。
状态转移:f[i][j] += f[i - 1][k],其中k为所有与j不存在相邻单元格颜色相同情况的状态。
初始化:f[0][j] = 1
class Solution {public int colorTheGrid(int n, int m) {final int MOD = (int)(1e9+7);List<String> list = new ArrayList<>();for (int i = 0; i < Math.pow(3, n); i++) { // 1String s = Integer.toString(i, 3);StringBuilder sb = new StringBuilder();int minus = n - s.length();while (minus-- > 0)sb.append("0");sb.append(s);s = sb.toString();if (check(s))list.add(s);}// System.out.println(list.size());Map<String, Integer> stoi = new HashMap<>(); //存一下字符串到下标的映射for (int i = 0; i < list.size(); i++)stoi.put(list.get(i), i);Map<String, List<String>> map = new HashMap<>(); // 2for (String s : list) {map.put(s, new ArrayList<>());List<String> ll = map.get(s);for (String t : list) {if (check(s, t))ll.add(t);}}int[][] f = new int[m][list.size()]; // 3Arrays.fill(f[0], 1);for (int i = 1; i < m; i++) {for (int j = 0; j < list.size(); j++) {String cur = list.get(j);for (String s : map.get(cur)) {f[i][j] = (f[i][j] + f[i - 1][stoi.get(s)]) % MOD;}}}int res = 0;for (int i = 0; i < list.size(); i++)res = (res + f[m - 1][i]) % MOD;return res;}boolean check(String s, String t) {for (int i = 0; i < s.length(); i++)if (s.charAt(i) == t.charAt(i))return false;return true;}boolean check(String s) {for (int i = 1; i < s.length(); i++) {if (s.charAt(i) == s.charAt(i - 1))return false;}return true;}}
注意转成3进制字符串是没有前导0的,得自己补一下!
本题的基础:1411. 给 N x 3 网格图涂色的方案数
1349. 参加考试的最大学生数
本题也可以用二分图来做,因为所有有关联的座位能完全转换成二分图。将所有座位转换成多组二分图,然后统计每组的最大能坐人数,累加后就是最终的答案。
枚举子集的状态压缩DP
1986. 完成任务的最少工作时间段
你被安排了 n 个任务。任务需要花费的时间用长度为 n 的整数数组 tasks 表示,第 i 个任务需要花费 tasks[i] 小时完成。一个 工作时间段 中,你可以 至多 连续工作 sessionTime 个小时,然后休息一会儿。
你需要按照如下条件完成给定任务:
- 如果你在某一个时间段开始一个任务,你需要在 同一个 时间段完成它。
- 完成一个任务后,你可以 立马 开始一个新的任务。
- 你可以按 任意顺序 完成任务。
给你 tasks 和 sessionTime ,请你按照上述要求,返回完成所有任务所需要的 最少 数目的 工作时间段 。
测试数据保证 sessionTime 大于等于 tasks[i] 中的 最大值 。
示例 1:
输入:tasks = [1,2,3], sessionTime = 3 输出:2 解释:你可以在两个工作时间段内完成所有任务。 - 第一个工作时间段:完成第一和第二个任务,花费 1 + 2 = 3 小时。 - 第二个工作时间段:完成第三个任务,花费 3 小时。
示例 2:
输入:tasks = [3,1,3,1,1], sessionTime = 8 输出:2 解释:你可以在两个工作时间段内完成所有任务。 - 第一个工作时间段:完成除了最后一个任务以外的所有任务,花费 3 + 1 + 3 + 1 = 8 小时。 - 第二个工作时间段,完成最后一个任务,花费 1 小时。
示例 3:
输入:tasks = [1,2,3,4,5], sessionTime = 15 输出:1 解释:你可以在一个工作时间段以内完成所有任务。
提示:
- n == tasks.length
- 1 <= n <= 14
- 1 <= tasks[i] <= 10
- max(tasks[i]) <= sessionTime <= 15
思路:
NP问题
使用子集枚举的状态压缩DP
状态表示:f[i]表示完成二进制位为1的所有任务的所有方案的集和
状态属性:完成所有任务使用的最少时间段的个数
状态转移:考虑更小的划分
如果所有任务能在一个时间段内完成:f[i] = 1;
如果所有任务不能在一个时间段内完成,考虑将任务分成两个子任务(子集的子集)f[i] = Math.min(f[i], f[j] + f[i ^ j])
因为是从小到大枚举子集,所以求当前状态时子任务的状态已经被求出了
初始化:f[i] = 0x3f3f3f3f, f[0] = 0, 所有能在一个时间段内完成的任务子集初始化为f[k] = 1
class Solution {public int minSessions(int[] tasks, int sessionTime) {int n = tasks.length, m = 1 << n;int[] f = new int[m];Arrays.fill(f, 0x3f3f3f3f);f[0] = 0;for (int i = 1; i < m; i++) {int sum = 0;for (int j = 0; j < n; j++)if ((i >> j & 1) == 1)sum += tasks[j];if (sum <= sessionTime)f[i] = 1;}for (int i = 0; i < m; i++) {for (int j = i; j > 0; j = (j - 1) & i) {f[i] = Math.min(f[i], f[j] + f[i ^ j]);}}return f[m - 1];}}
1655. 分配重复整数
给你一个长度为 n 的整数数组 nums ,这个数组中至多有 50 个不同的值。同时你有 m 个顾客的订单 quantity ,其中,整数 quantity[i] 是第 i 位顾客订单的数目。请你判断是否能将 nums 中的整数分配给这些顾客,且满足:
- 第 i 位顾客 恰好 有 quantity[i] 个整数。
- 第 i 位顾客拿到的整数都是 相同的 。
- 每位顾客都满足上述两个要求。
如果你可以分配 nums 中的整数满足上面的要求,那么请返回 true ,否则返回 false 。
示例 1:
输入:nums = [1,2,3,4], quantity = [2] 输出:false 解释:第 0 位顾客没办法得到两个相同的整数。
示例 2:
输入:nums = [1,2,3,3], quantity = [2] 输出:true 解释:第 0 位顾客得到 [3,3] 。整数 [1,2] 都没有被使用。
示例 3:
输入:nums = [1,1,2,2], quantity = [2,2] 输出:true 解释:第 0 位顾客得到 [1,1] ,第 1 位顾客得到 [2,2] 。
示例 4:
输入:nums = [1,1,2,3], quantity = [2,2] 输出:false 解释:尽管第 0 位顾客可以得到 [1,1] ,第 1 位顾客没法得到 2 个一样的整数。
示例 5:
输入:nums = [1,1,1,1,1], quantity = [2,3] 输出:true 解释:第 0 位顾客得到 [1,1] ,第 1 位顾客得到 [1,1,1] 。
提示:
- n == nums.length
- 1 <= n <= 105
- 1 <= nums[i] <= 1000
- m == quantity.length
- 1 <= m <= 10
- 1 <= quantity[i] <= 105
- nums 中至多有 50 个不同的数字。
思路:
NP问题
使用子集枚举的状态压缩DP
预处理:统计每个数字的次数count[x]
考虑一个数字能不能满足所有顾客,如果不能,再考虑两个数字能不能满足,以此类推知至最后一个数字
如果遍历到中间某一个数字能满足所有顾客,返回true即可
考虑当前遍历的最后一个数字能满足哪些顾客(子集的子集),如果剩余顾客能被前面的数字满足,说明当前枚举到的数字能满足该顾客子集
class Solution {public boolean canDistribute(int[] nums, int[] quantity) {List<Integer> list = new ArrayList<>();Arrays.sort(nums);int n = nums.length;for (int i = 0; i < n; i++) {int j = i;while (j + 1 < n && nums[j + 1] == nums[i])j++;list.add(j - i + 1);i = j;}n = list.size();int m = quantity.length;boolean[][] st = new boolean[n][1 << m];for (int i = 0; i < n; i++) {for (int j = 0; j < 1 << m; j++) {int sum = 0;for (int k = 0; k < m; k++) {if ((j >> k & 1) == 1)sum += quantity[k];}if (sum <= list.get(i))st[i][j] = true;}}boolean[][] f = new boolean[n][1 << m];for (int i = 0; i < n; i++) {for (int j = 0; j < 1 << m; j++) {f[i][j] = st[i][j];if (i > 0) {f[i][j] = f[i][j] || f[i - 1][j];for (int k = j; k > 0 && !f[i][j]; k = (k - 1) & j) {if (st[i][k])f[i][j] = f[i][j] || f[i - 1][j ^ k];}}}}return f[n - 1][(1 << m) - 1];}}
1494. 并行课程 II
给你一个整数 n 表示某所大学里课程的数目,编号为 1 到 n ,数组 dependencies 中, dependencies[i] = [xi, yi] 表示一个先修课的关系,也就是课程 xi 必须在课程 yi 之前上。同时你还有一个整数 k 。
在一个学期中,你 最多 可以同时上 k 门课,前提是这些课的先修课在之前的学期里已经上过了。
请你返回上完所有课最少需要多少个学期。题目保证一定存在一种上完所有课的方式。
示例 1: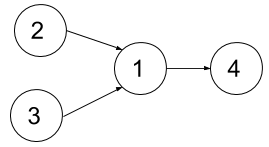
输入:n = 4, dependencies = [[2,1],[3,1],[1,4]], k = 2 输出:3 解释:上图展示了题目输入的图。在第一个学期中,我们可以上课程 2 和课程 3 。然后第二个学期上课程 1 ,第三个学期上课程 4 。
示例 2: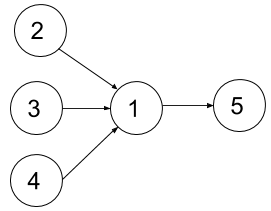
输入:n = 5, dependencies = [[2,1],[3,1],[4,1],[1,5]], k = 2 输出:4 解释:上图展示了题目输入的图。一个最优方案是:第一学期上课程 2 和 3,第二学期上课程 4 ,第三学期上课程 1 ,第四学期上课程 5 。
示例 3:
输入:n = 11, dependencies = [], k = 2 输出:6
提示:
- 1 <= n <= 15
- 1 <= k <= n
- 0 <= dependencies.length <= n * (n-1) / 2
- dependencies[i].length == 2
- 1 <= xi, yi <= n
- xi != yi
- 所有先修关系都是不同的,也就是说 dependencies[i] != dependencies[j] 。
- 题目输入的图是个有向无环图。
思路:
NP问题
使用子集枚举的状态压缩DP
预处理:每个课程的所有先修课程
每个课程集的所有先修课程(需满足该课程集课程个数小于等于k,该课程集与其先修课程集没有交集)
从小到大遍历每个子集,考虑最后一次选课的集和,如果能选,更新该子集的最小选法
class Solution {public int minNumberOfSemesters(int n, int[][] relations, int k) {int[] pre = new int[n];int[] pre_subset = new int[1 << n];boolean[] valid = new boolean[1 << n];// 预处理for (int[] p : relations) {int a = p[0] - 1, b = p[1] - 1;pre[b] |= 1 << a;}for (int i = 0; i < 1 << n; i++) {int cnt = 0;for (int j = 0; j < n; j++) {if ((i >> j & 1) == 1) {cnt++;pre_subset[i] |= pre[j];}}if (cnt <= k && (pre_subset[i] & i) == 0)valid[i] = true;}// 子集状压DPint[] f = new int[1 << n];Arrays.fill(f, 0x3f3f3f3f);f[0] = 0;for (int state = 0; state < 1 << n; state++) {for (int subset = state; subset > 0; subset = (subset - 1) & state) {if (valid[subset] && ((state ^ subset) & pre_subset[subset]) == pre_subset[subset])f[state] = Math.min(f[state], f[state ^ subset] + 1);}}return f[(1 << n) - 1];}}
1595. 连通两组点的最小成本
给你两组点,其中第一组中有 size1 个点,第二组中有 size2 个点,且 size1 >= size2 。
任意两点间的连接成本 cost 由大小为 size1 x size2 矩阵给出,其中 cost[i][j] 是第一组中的点 i 和第二组中的点 j 的连接成本。如果两个组中的每个点都与另一组中的一个或多个点连接,则称这两组点是连通的。换言之,第一组中的每个点必须至少与第二组中的一个点连接,且第二组中的每个点必须至少与第一组中的一个点连接。
返回连通两组点所需的最小成本。
示例 1: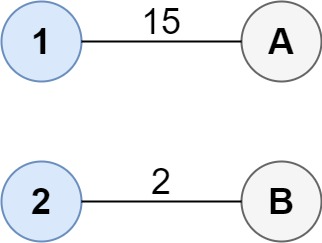
输入:cost = [[15, 96], [36, 2]] 输出:17 解释:连通两组点的最佳方法是: 1—A 2—B 总成本为 17 。
示例 2: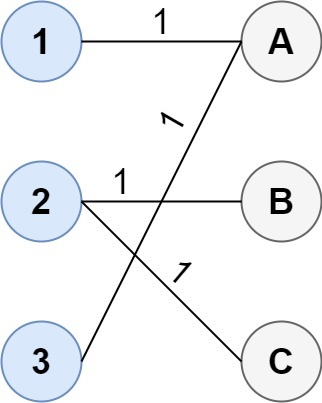
输入:cost = [[1, 3, 5], [4, 1, 1], [1, 5, 3]] 输出:4 解释:连通两组点的最佳方法是: 1—A 2—B 2—C 3—A 最小成本为 4 。 请注意,虽然有多个点连接到第一组中的点 2 和第二组中的点 A ,但由于题目并不限制连接点的数目,所以只需要关心最低总成本。
示例 3:
输入:cost = [[2, 5, 1], [3, 4, 7], [8, 1, 2], [6, 2, 4], [3, 8, 8]] 输出:10
提示:
- size1 == cost.length
- size2 == cost[i].length
- 1 <= size1, size2 <= 12
- size1 >= size2
- 0 <= cost[i][j] <= 100
思路:
状压DP
状态表示:f[i][j]表示考虑size1前i个数,连接到j中位为1的size2中的数的所有方案
集和属性:最小代价
状态转移:考虑第i个数连到哪里
1. `j`的某个非空子集`k`,且前`i - 1`个数连接到`j ^ k`2. `j`中的某个数,且前`i - 1`个数连接到`j`
:::tips b比较难想到!需要仔细分析一下! :::
class Solution {public int connectTwoGroups(List<List<Integer>> cost) {int n = cost.size(), m = cost.get(0).size();int[][] g = new int[n + 1][1 << m];int[][] min = new int[n + 1][1 << m];for (int i = 1; i <= n; i++) {List<Integer> list = cost.get(i - 1);for (int j = 0; j < 1 << m; j++) {int sum = 0;int v = 0x3f3f3f3f;for (int k = 0; k < m; k++) {if ((j >> k & 1) == 1) {sum += list.get(k);v = Math.min(v, list.get(k));}}g[i][j] = sum;min[i][j] = v;}}int[][] f = new int[n + 1][1 << m];for (int i = 0; i <= n; i++)Arrays.fill(f[i], 0x3f3f3f3f);f[0][0] = 0;for (int i = 1; i <= n; i++) {for (int j = 0; j < 1 << m; j++) {for (int k = j; k > 0; k = (k - 1) & j) {f[i][j] = Math.min(f[i][j], f[i - 1][j ^ k] + g[i][k]);}f[i][j] = Math.min(f[i][j], f[i - 1][j] + min[i][j]);}}return f[n][(1 << m) - 1];}}
| 691. 贴纸拼词 | |
|---|---|
| 943. 最短超级串 | |
| 1125. 最小的必要团队 | |
| 1994. 好子集的数目 | |
| zj-future04. 门店商品调配 | 和为0的子集枚举 |

