周赛 - 🏆 第 297 场力扣周赛 - 《学习笔记》

5259. 计算应缴税款总额
5270. 网格中的最小路径代价
5289. 公平分发饼干
6094. 公司命名

只能说大起之后必有大落，不过t4最后还是自己做出来的。

5259. 计算应缴税款总额

给你一个下标从 0 开始的二维整数数组 brackets ，其中 brackets[i] = [upperi, percenti] ，表示第 i 个税级的上限是 upperi ，征收的税率为 percenti 。税级按上限 从低到高排序（在满足 0 < i < brackets.length 的前提下，upperi-1 < upperi）。
税款计算方式如下：

不超过 upper0 的收入按税率 percent0 缴纳
接着 upper1 - upper0 的部分按税率 percent1 缴纳
然后 upper2 - upper1 的部分按税率 percent2 缴纳
以此类推

给你一个整数 income 表示你的总收入。返回你需要缴纳的税款总额。与标准答案误差不超 10-5 的结果将被视作正确答案。

示例 1：
输入：brackets = [[3,50],[7,10],[12,25]], income = 10 输出：2.65000 解释： 前 $3 的税率为 50% 。需要支付税款 $3 50% = $1.50 。接下来 $7 - $3 = $4 的税率为 10% 。需要支付税款 $4 10% = $0.40 。最后 $10 - $7 = $3 的税率为 25% 。需要支付税款 $3 25% = $0.75 。需要支付的税款总计 $1.50 + $0.40 + $0.75 = $2.65 。
示例 2：
输入：brackets = [[1,0],[4,25],[5,50]], income = 2 输出：0.25000 解释： 前 $1 的税率为 0% 。需要支付税款 $1 0% = $0 。剩下 $1 的税率为 25% 。需要支付税款 $1 25% = $0.25 。需要支付的税款总计 $0 + $0.25 = $0.25 。
示例 3：
输入：brackets = [[2,50]], income = 0 输出：0.00000 *解释：没有收入，无需纳税，需要支付的税款总计 $0 。

提示：

1 <= brackets.length <= 100
1 <= upperi <= 1000
0 <= percenti <= 100
0 <= income <= 1000
upperi 按递增顺序排列
upperi 中的所有值 互不相同
最后一个税级的上限大于等于 income

思路：
按要求计算即可

class Solution {
    public double calculateTax(int[][] b, int s) {
        int p = 0;
        int x = 0;
        double res = 0;
        for (int[] v : b) {
            if (s >= v[0]) {
                res += 1.0 * (v[0] - x) * (v[1] / 100.0);
                x = v[0];
            } else {
                p = v[1];
                break;
            }
        }
        res += 1.0 * (s - x) * (p / 100.0);
        return res;
    }
}

5270. 网格中的最小路径代价

给你一个下标从 0 开始的整数矩阵 grid ，矩阵大小为 m x n ，由从 0 到 m n - 1 的不同整数组成。你可以在此矩阵中，从一个单元格移动到 下一行 的任何其他单元格。如果你位于单元格 (x, y) ，且满足 x < m - 1 ，你可以移动到 (x + 1, 0), (x + 1, 1), …, (x + 1, n - 1) 中的任何一个单元格。注意： 在最后一行中的单元格不能触发移动。
每次可能的移动都需要付出对应的代价，代价用一个下标从 0 开始的二维数组 moveCost 表示，该数组大小为 (m n) x n ，其中 moveCost[i][j] 是从值为 i 的单元格移动到下一行第 j 列单元格的代价。从 grid 最后一行的单元格移动的代价可以忽略。
grid 一条路径的代价是：所有路径经过的单元格的 值之和 加上所有移动的 代价之和 。从 第一行 任意单元格出发，返回到达 最后一行 任意单元格的最小路径代价。

示例 1：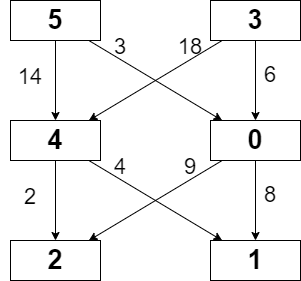

输入：grid = [[5,3],[4,0],[2,1]], moveCost = [[9,8],[1,5],[10,12],[18,6],[2,4],[14,3]] 输出：17 解释：最小代价的路径是 5 -> 0 -> 1 。 - 路径途经单元格值之和 5 + 0 + 1 = 6 。 - 从 5 移动到 0 的代价为 3 。 - 从 0 移动到 1 的代价为 8 。路径总代价为 6 + 3 + 8 = 17 。
示例 2：
输入：grid = [[5,1,2],[4,0,3]], moveCost = [[12,10,15],[20,23,8],[21,7,1],[8,1,13],[9,10,25],[5,3,2]] 输出：6 解释： 最小代价的路径是 2 -> 3 。 - 路径途经单元格值之和 2 + 3 = 5 。 - 从 2 移动到 3 的代价为 1 。路径总代价为 5 + 1 = 6 。

提示：

m == grid.length
n == grid[i].length
2 <= m, n <= 50
grid 由从 0 到 m * n - 1 的不同整数组成
moveCost.length == m * n
moveCost[i].length == n
1 <= moveCost[i][j] <= 100

思路：
线性DP

class Solution {
    public int minPathCost(int[][] g, int[][] moveCost) {
        int n = g.length, m = g[0].length;
        int[][] f = new int[n][m];
        for (int i = 0; i < m; i++)
            f[0][i] = g[0][i];
        for (int i = 1; i < n; i++)
            Arrays.fill(f[i], 0x3f3f3f3f);
        for (int i = 0; i < n - 1; i++) {
            for (int j = 0; j < m; j++) {
                int x = g[i][j];
                for (int k = 0; k < m; k++) {
                    f[i + 1][k] = Math.min(f[i + 1][k], f[i][j] + moveCost[x][k] + g[i + 1][k]);
                }
            }
        }
        int min = 0x3f3f3f3f;
        for (int i = 0; i < m; i++)
            min = Math.min(min, f[n - 1][i]);
        return min;
    }
}

5289. 公平分发饼干

给你一个整数数组 cookies ，其中 cookies[i] 表示在第 i 个零食包中的饼干数量。另给你一个整数 k 表示等待分发零食包的孩子数量，所有零食包都需要分发。在同一个零食包中的所有饼干都必须分发给同一个孩子，不能分开。
分发的 不公平程度 定义为单个孩子在分发过程中能够获得饼干的最大总数。
返回所有分发的最小不公平程度。

示例 1：
输入：cookies = [8,15,10,20,8], k = 2 输出：31 解释：一种最优方案是 [8,15,8] 和 [10,20] 。 - 第 1 个孩子分到 [8,15,8] ，总计 8 + 15 + 8 = 31 块饼干。 - 第 2 个孩子分到 [10,20] ，总计 10 + 20 = 30 块饼干。分发的不公平程度为 max(31,30) = 31 。可以证明不存在不公平程度小于 31 的分发方案。
示例 2：
输入：cookies = [6,1,3,2,2,4,1,2], k = 3 输出：7 解释：一种最优方案是 [6,1]、[3,2,2] 和 [4,1,2] 。 - 第 1 个孩子分到 [6,1] ，总计 6 + 1 = 7 块饼干。 - 第 2 个孩子分到 [3,2,2] ，总计 3 + 2 + 2 = 7 块饼干。 - 第 3 个孩子分到 [4,1,2] ，总计 4 + 1 + 2 = 7 块饼干。分发的不公平程度为 max(7,7,7) = 7 。可以证明不存在不公平程度小于 7 的分发方案。

提示：

2 <= cookies.length <= 8
1 <= cookies[i] <= 105
2 <= k <= cookies.length

思路：
方法1：回溯
方法2：状态压缩DP
第一种：考虑所有物品的子集x，枚举x的所有子集，计算将x分给k个人的最小最大代价
第二种：考虑前k个人，瓜分所有饼干的最小最大代价
方法3：二分+ 状态压缩
二分最大代价(左界 = 饼干数量的最大值，右界 = 饼干的和)
二分代码块内计算该瓜分所需的最小人数，由此判断下一步动作

class Solution {
    int[] sum = new int[8];
    int k;
    int[] c;
    int ans = 0x3f3f3f3f;
    public int distributeCookies(int[] c, int k) {
        this.c = c;
        this.k = k;
        dfs(0);
        return ans;
    }
    void dfs(int u) {
        if (u == c.length) {
            int max = 0;
            for (int i = 0; i < k; i++)
                max = Math.max(max, sum[i]);
            ans = Math.min(ans, max);
            return;
        }
        for (int i = 0; i < k; i++) {
            sum[i] += c[u];
            dfs(u + 1);
            sum[i] -= c[u];
        }
    }
}
// 回溯+ 剪枝
class Solution {
    int[] c;
    int k;
    int[] s = new int[8];
    public int distributeCookies(int[] c, int k) {
        this.c = c;
        this.k = k;
        Arrays.sort(c);
        int max = 0, sum = 0;
        for (int x : c) {
            max = Math.max(x, max);
            sum += x;
        }
        int l = max, r = sum;
        while (l < r) {
            int mid = l + r >> 1;
            Arrays.fill(s, 0);
            if (dfs(c.length - 1, mid))
                r = mid;
            else
                l = mid + 1;
        }
        return l;
    }
    boolean dfs(int u, int t) {
        if (u < 0) {
            return true;
        }
        Set<Integer> set = new HashSet<>();
        for (int i = 0; i < k; i++) {
            if (s[i] + c[u] > t || set.contains(s[i])) continue;
            set.add(s[i]);
            s[i] += c[u];
            if (dfs(u - 1, t))
                return true;
            s[i] -= c[u];
            if (s[i] == 0 || s[i] + c[u] == t)
                break;
        }
        return false;
    }
}

// 状压DP
// 从物品角度
class Solution {
    public int distributeCookies(int[] cookies, int K) {
        int n = cookies.length;
        int[][] f = new int[1 << n][K + 1];
        for (int i = 0; i < 1 << n; i++) Arrays.fill(f[i], 0x3f3f3f3f);
        f[0][0] = 0;
        for (int i = 0; i < 1 << n; i++) {
            for (int k = 1; k <= K; k++) {
                for (int st = i; st > 0; st = i & (st - 1)) {
                    int t = 0;
                    for (int j = 0; j < n; j++)
                        if ((st >> j & 1) == 1)
                            t += cookies[j];
                    f[i][k] = Math.min(f[i][k], Math.max(f[i ^ st][k - 1], t));
                }
                f[i][k] = Math.min(f[i][k], f[i][k - 1]);
            }
        }
        return f[(1 << n) - 1][K];
    }
}

// 状压DP
// 从人的角度
class Solution {
    public int distributeCookies(int[] c, int k) {
        int n = c.length;
        int[] s = new int[1 << n];
        // for (int i = 0; i < 1 << n; i++) {
        //     int sum = 0;
        //     for (int j = 0; j < n; j++)
        //         if ((i >> j & 1) == 1)
        //             sum += c[j];
        //     s[i] = sum;
        // }
        // 另一种预处理方法
        for (int i = 0; i < n; i++) {
            for (int u = 1 << i, j = 0; j < u; j++)
                s[u | j] = s[j] + c[i];
        }
        // 另一种预处理方法，更快
        for (int i = 0; i < 1 << n; i++) {
            for (int j = 0; j < n; j++) {
                if ((i >> j & 1) == 1) {
                    s[i] = s[i ^ (1 << j)] + c[j];
                    break;
                }
            }
        }
        int[] f = new int[1 << n];
        Arrays.fill(f, Integer.MAX_VALUE);
        f[0] = 0;
        for (int i = 1; i <= k; i++) {
            for (int st = (1 << n) - 1; st > 0; st--) {
                for (int j = st; j > 0; j = st & (j - 1))
                    f[st] = Math.min(f[st], Math.max(f[st ^ j], s[j]));
            }
        }
        return f[(1 << n) - 1];
    }
}

// 二分 + 状态压缩
class Solution {
    public int distributeCookies(int[] c, int k) {
        int n = c.length;
        int[] s = new int[1 << n];
        for (int i = 0; i < 1 << n; i++) {
            for (int j = 0; j < n; j++)
                if ((i >> j & 1) != 1)
                    continue;
                else {
                    s[i] = s[i ^ (1 << j)] + c[j];
                    break;
                }
        }
        int[] f = new int[1 << n];
        int l = Arrays.stream(c).max().getAsInt(), r = Arrays.stream(c).sum();
        while (l < r) {
            int mid = l + r >> 1;
            Arrays.fill(f, 0x3f3f3f3f);
            f[0] = 0;
            for (int i = 0; i < 1 << n; i++) {
                for (int st = i; st > 0; st = i & (st - 1)) {
                    if (s[st] <= mid)
                        f[i] = Math.min(f[i], f[st ^ i] + 1);
                }
            }
            if (f[(1 << n) - 1] > k)
                l = mid + 1;
            else
                r = mid;
        }
        return l;
    }
}

6094. 公司命名

给你一个字符串数组 ideas 表示在公司命名过程中使用的名字列表。公司命名流程如下：

从 ideas 中选择 2 个不同名字，称为 ideaA 和 ideaB 。
交换 ideaA 和 ideaB 的首字母。
如果得到的两个新名字都不在 ideas 中，那么 ideaA ideaB（串联 ideaA 和 ideaB ，中间用一个空格分隔）是一个有效的公司名字。
否则，不是一个有效的名字。

返回不同且有效的公司名字的数目。

示例 1：
输入：ideas = [“coffee”,”donuts”,”time”,”toffee”] 输出：6 解释：下面列出一些有效的选择方案： - (“coffee”, “donuts”)：对应的公司名字是 “doffee conuts” 。 - (“donuts”, “coffee”)：对应的公司名字是 “conuts doffee” 。 - (“donuts”, “time”)：对应的公司名字是 “tonuts dime” 。 - (“donuts”, “toffee”)：对应的公司名字是 “tonuts doffee” 。 - (“time”, “donuts”)：对应的公司名字是 “dime tonuts” 。 - (“toffee”, “donuts”)：对应的公司名字是 “doffee tonuts” 。因此，总共有 6 个不同的公司名字。下面列出一些无效的选择方案： - (“coffee”, “time”)：在原数组中存在交换后形成的名字 “toffee” 。 - (“time”, “toffee”)：在原数组中存在交换后形成的两个名字。 - (“coffee”, “toffee”)：在原数组中存在交换后形成的两个名字。
示例 2：
输入：ideas = [“lack”,”back”] 输出：0 解释：不存在有效的选择方案。因此，返回 0 。

提示：

2 <= ideas.length <= 5 * 104
1 <= ideas[i].length <= 10
ideas[i] 由小写英文字母组成
ideas 中的所有字符串 互不相同

思路：
考虑每对字符相互替换的方案数
时间复杂度：O(∣Σ∣2_n_)

class Solution {
    public long distinctNames(String[] ideas) {
        Map<String, Integer> map = new HashMap<>();
        for (String s : ideas) {
            String t = s.substring(1, s.length());
            int idx = s.charAt(0) - 'a';
            map.putIfAbsent(t, 0);
            int x = map.get(t);
            x |= 1 << idx;
            map.put(t, x);
        }
        int[][] c = new int[26][26];
        for (String s : map.keySet()) {
            int x = map.get(s);
            for (int i = 0; i < 26; i++) {
                if ((x >> i & 1) != 1) continue;
                for (int j = 0; j < 26; j++) {
                    if (i == j) continue;
                    if ((x >> j & 1) == 0)
                            c[i][j]++;
                }
            }
        }
        long res = 0;
        for (int i = 0; i < 26; i++)
            for (int j = 0; j < 26; j++)
                res += 1L * c[i][j] * c[j][i];
        return res;
    }
}