三角形的最小路径和-120

给定一个三角形 triangle ，找出自顶向下的最小路径和。

每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说，如果正位于当前行的下标 i ，那么下一步可以移动到下一行的下标 i 或 i + 1 。

示例 1：

Input: triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
Output: 11
Explanation: The triangle looks like:
   2
  3 4
 6 5 7
4 1 8 3
The minimum path sum from top to bottom is 2 + 3 + 5 + 1 = 11 (underlined above).

示例 2：

Input: triangle = [[-10]]
Output: -10

提示：

• 1 ≤ triangle.length ≤ 200
• triangle[0].length == 1
• triangle[i].length == triangle[i-1].length + 1
• -10 ≤ triangle[i][j] ≤ 10

思路

我们新建一个二维dp[][]数组，里面的值含义是：到达当前位置的最小路径和。

我们假设输入的三角形为：

[
    [2],
    [3, 4],
    [6, 5, 7],
    [4, 1, 8, 3],
]

• 假设三角形只有 1 行，那么dp[0][0] = triangle[0][0]；
• 假设三角形有 2 行，那么dp[1][0] = triangle[0][0] + triangle[1][0]，也就是位于 (1, 0) 的最小路径和只能是从它头顶上的那个元素来的；dp[1][1] = triangle[0][0] + triangle[1][1]，也就是位于 (1, 1) 的最小路径和只能是从它西北方向来的。

• 当三角形有 row 行时，我们发现一个规律，最左边那一列的dp值只能是从它头上来的，所以我们可以先写一个for循环把最左边那一列的dp值确定下来：cpp dp[0][0] = triangle[0][0]; for(int i = 1; i < triangle.size(); i++) dp[i][0] = dp[i-1][0] + triangle[i][0];

• 观察下图：

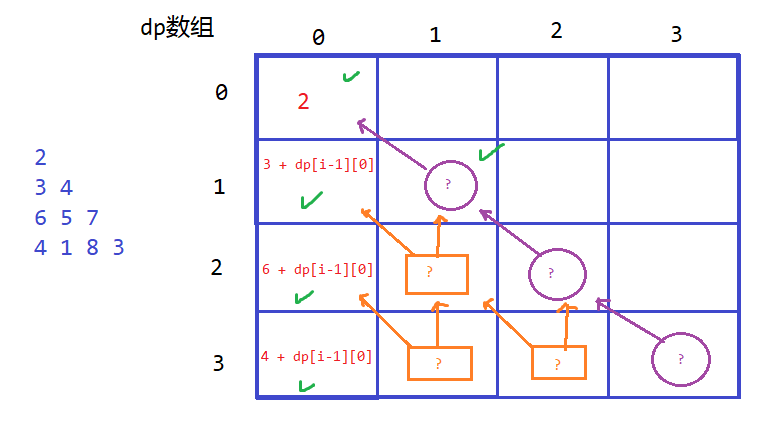
• 打绿色勾的是我们上前面几步初始化好的值。橙色方框的值是由北方向和西北方向的最小值确定；紫色圆圈的值仅有西北方向的dp值确定。我们可以根据初始化好的值来写递推公式：(j)%20%3D%20%0A%5Cbegin%7Bcases%7D%0Amin%5C%7B%5C%20dp(i-1)(j)%20%2B%20triangle%5Bi%5D%5Bj%5D%2C%5C%20dp(i-1)(j-1)%20%2B%20triangle%5Bi%5D%5Bj%5D%5C%20%5C%7D%0A%2C%26%20i%20%5Cge%202%2C%20j%20%5Cne%200%20%E4%B8%94%5C%20j%5C%20%E4%B8%8D%E4%B8%BA%E9%98%9F%E5%B0%BE%E5%85%83%E7%B4%A0%0A%5C%5C%0Atriangle%5Bi%5D%5Bj%5D%20%2B%20dp(i-1)(j-1)%0A%2C%26%20i%5Cge%201%2C%20j%5C%20%E4%B8%BA%E9%98%9F%E5%B0%BE%E5%85%83%E7%B4%A0%0A%5Cend%7Bcases%7D%0A#card=math&code=dp%28i%29%28j%29%20%3D%20%0A%5Cbegin%7Bcases%7D%0Amin%5C%7B%5C%20dp%28i-1%29%28j%29%20%2B%20triangle%5Bi%5D%5Bj%5D%2C%5C%20dp%28i-1%29%28j-1%29%20%2B%20triangle%5Bi%5D%5Bj%5D%5C%20%5C%7D%0A%2C%26%20i%20%5Cge%202%2C%20j%20%5Cne%200%20%E4%B8%94%5C%20j%5C%20%E4%B8%8D%E4%B8%BA%E9%98%9F%E5%B0%BE%E5%85%83%E7%B4%A0%0A%5C%5C%0Atriangle%5Bi%5D%5Bj%5D%20%2B%20dp%28i-1%29%28j-1%29%0A%2C%26%20i%5Cge%201%2C%20j%5C%20%E4%B8%BA%E9%98%9F%E5%B0%BE%E5%85%83%E7%B4%A0%0A%5Cend%7Bcases%7D%0A)

根据递推公式填写完表后，变量最后一行的dp[][]数组，返回最小值即可。

代码

class Solution {
public:
    int minimumTotal(vector<vector<int>>& triangle) {
        if( triangle.size() == 0 )   return 0;
        if( triangle.size() == 1 )   return triangle[0][0];
        vector<vector<int>> dp(triangle.size(), vector<int>( triangle[ triangle.size()-1 ].size() ));
        dp[0][0] = triangle[0][0];
        dp[1][1] = triangle[0][0] + triangle[1][1];
        for(int i = 1; i < triangle.size(); i++)   dp[i][0] = dp[i-1][0] + triangle[i][0];
        for(int i = 2; i < triangle.size(); i++) {
            for(int j = 1; j < triangle[i].size()-1; j++) {
                int from_north = dp[i-1][j] + triangle[i][j];
                int from_northwest = dp[i-1][j-1] + triangle[i][j];
                dp[i][j] = from_north < from_northwest ? from_north : from_northwest;
            }
            dp[i][ triangle[i].size()-1 ] = dp[i-1][triangle[i].size()-2] + triangle[i][ triangle[i].size()-1 ];
        }
        int MIN = *min_element( dp[ triangle.size()-1 ].begin(), dp[ triangle.size()-1 ].end() );
        return MIN;
    }
};