螺旋矩阵Ⅱ-59

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1：

Input: n = 3
Output: [[1,2,3],[8,9,4],[7,6,5]]

示例 2：

Input: n = 1
Output: [[1]]

提示：

• 1 ≤ n ≤ 20；

思路

学习Krahets神的思路，他的边界处理很优秀。

示意图如下：

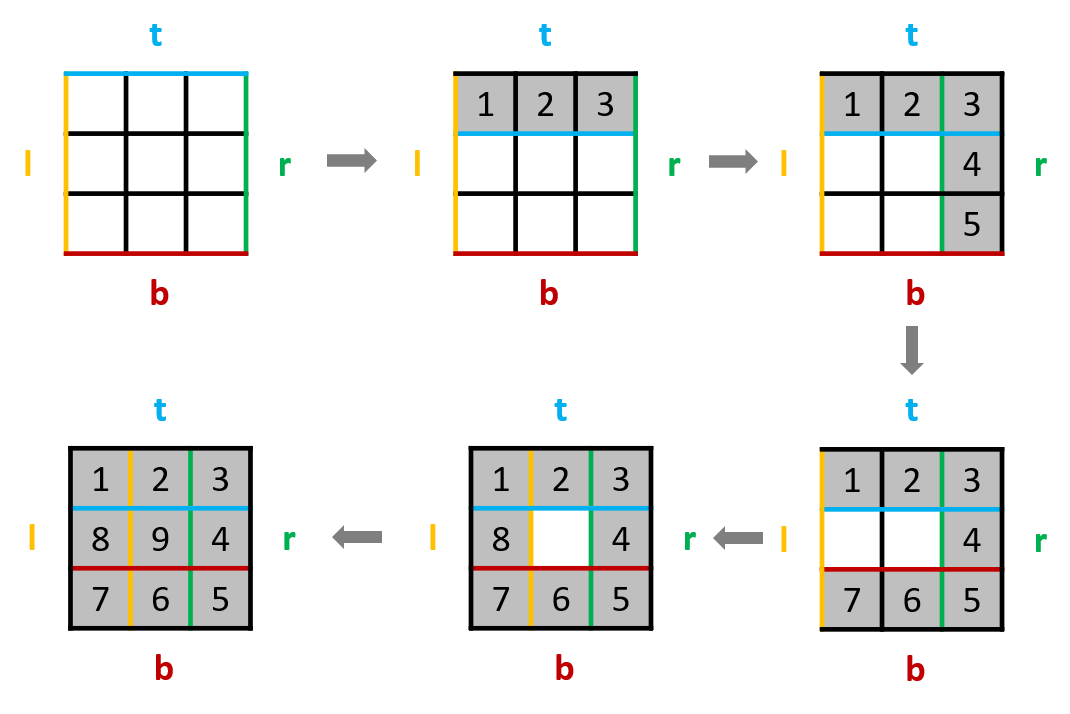
我们新建4个边界：top_edge = 0、bottom_edge = n - 1、left_edge = 0、right_edge = n - 1，模拟整个填数的过程。用while()循环来填数，第一个数是1，当我们填数填到n*n就停止。

在while()循环里分四个步骤：

1. 从左往右填数，填完后top_edge += 1；
2. 从上往下填数，填完后right_edge -=1；
3. 从右往左填数，填完后bottom_edge -=1；
4. 从下往上填数，填完后left_edge += 1；

代码

Cpp：

// 0ms, 6.3MB
class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        vector<vector<int>> matrix(n, vector<int>(n));
        int left_edge = 0;
        int right_edge = n - 1;
        int top_edge = 0;
        int bottom_edge = n - 1;
        int num = 1, target = n * n;
        while(num <= target) {
            // left to right
            for(int i = left_edge; i <= right_edge; i++)
                matrix[top_edge][i] = num ++;
            top_edge += 1;
            // top tp down
            for(int i = top_edge; i <= bottom_edge; i++) 
                matrix[i][right_edge] = num ++;
            right_edge -= 1;
            // right to left
            for(int i = right_edge; i >= left_edge; i--)
                matrix[bottom_edge][i] = num ++;
            bottom_edge -= 1;
            // bottom to top
            for(int i = bottom_edge; i >= top_edge; i--) 
                matrix[i][left_edge] = num ++;
            left_edge += 1;
        }
        return matrix;
    }
};

Rust：

// 0ms, 2.1MB
impl Solution {
    pub fn generate_matrix(n: i32) -> Vec<Vec<i32>> {
        let n = n as usize;
        let mut matrix: Vec<Vec<i32>> = vec![ vec![0; n]; n ];
        if n == 1 {
            matrix[0][0] = 1;
            return matrix;
        }
        let mut top_edge = 0;
        let mut bottom_edge = n - 1;
        let mut left_edge = 0;
        let mut right_edge = n - 1;
        let mut num: i32 = 1;
        let target: i32 = (n * n) as i32;
        let mut i = 0;
        while num <= target {
            // Left to right
            i = left_edge;
            while i <= right_edge {
                matrix[top_edge][i] = num;
                num += 1;
                i += 1;
            }
            top_edge += 1;
            // Top to bottom
            i = top_edge;
            while i <= bottom_edge {
                matrix[i][right_edge] = num;
                num += 1;
                i += 1;
            }
            right_edge -= 1;
            // Right to left
            i = right_edge;
            while i >= left_edge {
                matrix[bottom_edge][i] = num;
                num += 1;
                if i == 0 { break; }
                i -= 1;
            }
            bottom_edge -= 1;
            // Bottom to top
            i = bottom_edge;
            while i >= top_edge {
                matrix[i][left_edge] = num;
                num += 1;
                if i == 0 { break; }
                i -= 1;
            }
            left_edge += 1;
        }
        matrix
    }
}