基于 Perception 感知器算法实现鸢尾花二分类

    1. import numpy as np
    2. import pandas as pd
    1. data = pd.read_csv(r"dataset/iris.arff.csv", header=0)
    2. # data.head(10)
    3. # data.tail(10)
    4. # print(data.sample(10))
    5. # data = data.drop("Id",axis=1)  # 删除列
    6. print(len(data))
    7. if data.duplicated().any(): # 重复值
    8.     data.drop_duplicates(inplace=True) #删除重复值
    9.     print(len(data))
    10. display(data["class"].value_counts()) # 计算每个类别的数量
    11. # 因为感知器映射结果为1和-1，所以这里这也处理
    12. data["class"] = data["class"].map({"Iris-versicolor":0,"Iris-setosa":-1,"Iris-virginica":1}) # 类别名称映射为数字
    13. data = data[data["class"]!=0]
    14. len(data)

    150
    147

    Iris-versicolor 50
    Iris-virginica 49
    Iris-setosa 48
    Name: class, dtype: int64

    Out[8]: 97

    1. class Perception:
    2.     '''感知器算法实现。二分类'''
    3.     def __init__(self, learning_rate, times):
    4.         '''初始化
    6.         Parameters
    7.         -----
    8.         learning_rate: float 学习率
    9.         times: int 迭代次数
    10.         '''
    11.         self.learning_rate = learning_rate
    12.         self.times =  times
    13.     def step(self, z):
    14.         '''阶跃函数
    16.         Paraammeters
    17.         -----
    18.         z: 数组类型(或者是标量) 阶跃函数参数。将z映射为1或者-1
    20.         Return
    21.         -----
    22.         value: int z>0返回1.z<0返回1
    23.         '''
    24.         return np.where(z>0, 1,-1) # 一步实现对数值或者数组的计算返回
    25.     def fit(self, X, y):
    26.         '''训练
    28.         Parameters
    29.         -----
    30.         X: 特征矩阵，可以是List也可以是Ndarray，形状为： [样本数量,特征数量]
    31.         y: 标签数组
    32.         '''
    33.         X = np.asarray(X)
    34.         y = np.asarray(y)
    35.         # 创建权重向量。初始值为0。长度比特征多1.多出的是截距
    36.         self.w_ = np.zeros(1 + X.shape[1])
    37.         # 创建损失列表，用来保存每次迭代后的损失值
    38.         self.loss_ = []
    39.         for i in range(self.times):
    40.             # 感知器与逻辑回归的区别：逻辑回归中。使用所有样本计算梯度来更新权重。
    41.             # 而感知器是使用单个样本，依次计算梯度更新权重
    42.             loss = 0
    43.             for x,target in zip(X,y):
    44.                 # 计算预测值
    45.                 y_hat = self.step(np.dot(x, self.w_[1:]) + self.w_[0])
    46.                 # 如果预测值不等于目标值，返回1，loss+1，否则loss不增加
    47.                 loss += y_hat != target
    48.                 # 更新权重
    49.                 # w(j) = w(j) + 学习率 * (真实值-预测值)*x(j)
    50.                 self.w_[0] += self.learning_rate * (target - y_hat)
    51.                 self.w_[1:] +=  self.learning_rate * (target - y_hat) * x
    52.             # 将循环累计误差值增加到误差列表中
    53.             self.loss_.append(loss)
    54.     def predit(self, X):
    55.         '''根据参数预测
    57.         Parametres:
    58.         X: 特征矩阵，可以是List也可以是Ndarray，形状为： [样本数量,特征数量]
    60.         Return
    61.         -----
    62.         value: 数组类型， 分类值[1或-1]
    63.         '''
    64.         return self.step(np.dot(X, self.w_[1:]) + self.w_[0])
    1. t1 = data[data["class"]==1]
    2. t2 = data[data["class"]==-1]
    3. t1.sample(len(t1), random_state=0)
    4. t2.sample(len(t2), random_state=0)
    5. train_X = pd.concat([t1.iloc[:40,:-1], t2.iloc[:40, :-1]], axis=0)
    6. train_y = pd.concat([t1.iloc[:40,-1], t2.iloc[:40, -1]], axis=0)
    7. test_X = pd.concat([t1.iloc[40:,:-1], t2.iloc[40:, :-1]], axis=0)
    8. test_y = pd.concat([t1.iloc[40:,-1], t2.iloc[40:, -1]], axis=0)
    10. p = Perception(0.1, 10)
    11. p.fit(train_X,train_y)
    12. result = p.predit(test_X)
    13. # result
    14. display(result)
    15. display(test_y.values)
    16. display(p.w_)
    17. display(p.loss_) # 可以看出每次迭代后损失值就下降了

    array([ 1, 1, 1, 1, 1, 1, 1, 1, 1, -1, -1, -1, -1, -1, -1, -1, -1])

    array([ 1, 1, 1, 1, 1, 1, 1, 1, 1, -1, -1, -1, -1, -1, -1, -1, -1], dtype=int64)

    array([-0.2 , -0.5 , -0.68, 1.56, 0.88])

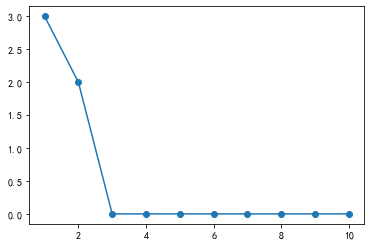
    [3, 2, 0, 0, 0, 0, 0, 0, 0, 0]

    1. import matplotlib as mpl
    2. import matplotlib.pyplot as plt
    3. mpl.rcParams["font.family"] = "SimHei"
    4. mpl.rcParams["axes.unicode_minus"] = False # 显示负号
    1. # 绘制真实值
    2. plt.plot(test_y.values, "go", ms=15, label="真实值")
    3. plt.plot(result, "rx", ms=15, label="预测值")
    4. plt.title("感知器二分类")
    5. plt.xlabel("样本序号")
    6. plt.xlabel("类别")
    7. plt.show()

    image.png

    1. # 绘制目标函数损失值
    2. plt.plot(range(1, p.times+1), p.loss_, "o-")

    []

    image.png