红黑树就是为了优化2354树

红黑树性质

  • 性质1：节点是红色或黑色
  • 性质2：根节点是黑色的
  • 性质3：每个红色节点的两个子节点都是黑色（从每个叶子到根的所有路径上不能有两个连续的红色节点）
  • 性质4：从任何一节点到其他每个叶子的所有路径都包含相同数目的黑色节点

    性质看不懂，来看234树转换为红黑树

    234树转红黑树示意图：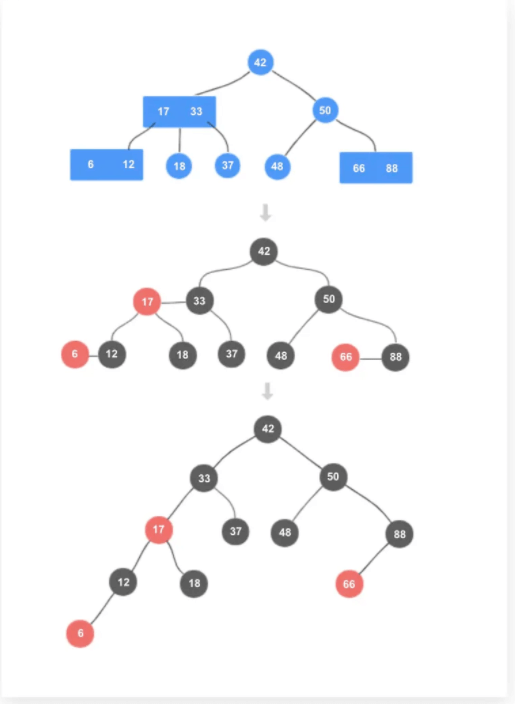
    image.png
    从上图你能看出红色节点是与黑色节点是同级的，又与黑球组合一起实现234树中的多个数据项，这也是性质四中为啥只看黑色节点的原因
    红色节点可以看做是虚拟节点，当与其他节点组合才会组成234树中的多项数据
    性质三种不能有连续的红色节点与红色节点下两个黑色节点。你看一个234树中数据项有三个，而红色与其他节点组合成为234树中的数据项，要是有两个连续红色节点，那数据项里怎吗弄？
    说白就是通过红色节点来实现234树中的多叉与单个节点中存在多个数据值，这些都是逻辑上实现的，物理上它还是二叉树，红黑树就是利用234树永远是平衡的这个特点

总结

红黑树就是普普通通的二叉平衡树，只是节点的意义不一样罢了
二叉平衡树的实现代码

  1. class Node {
  2.     constructor(value) {
  3.         this.value = value;
  4.         this.left = null;
  5.         this.right = null;
  6.     }
  7. }
  9. const node9 = new Node('9');
  10. const node8 = new Node('8');
  11. const node7 = new Node('7');
  12. const node6 = new Node('6');
  13. const node5 = new Node('5');
  14. const node4 = new Node('4');
  16. node9.left = node6;
  17. node6.left = node5;
  18. node5.left = node4;
  19. node6.right = node7;
  20. node7.right = node8;
  22. /**
  23.  * 利用单旋将二叉不平衡树变为二叉平衡树
  24.  * @param {*} root 跟节点
  25.  * @returns 返回平衡之后的根节点
  26.  */
  27. function change(root) {
  28.     if (isBalanceTree(root)) return root; // 返回平衡之后的根节点
  29.     // 走到这说明不是二叉平衡树
  30.     // 判断平不平衡需要从下往上判断
  31.     // 判断对二叉树进行平衡操作要按照后序遍历的顺序
  32.     // 后序遍历 先左子树 后右子树 最后自己
  33.     // 为何进行后序遍历，当根节点不是二叉平衡树，可能对子树进行单旋操作就成为二叉平衡树
  34.     if (root.left != null) root.left = change(root.left); // change函数会返回平衡之后的跟节点，故需要接收返回的的根节点
  35.     if (root.right != null) root.right = change(root.right);// change函数会返回平衡之后的跟节点，故需要接收返回的的根节点
  36.     // 获取深度
  37.     let leftTree = getDeep(root.left);
  38.     let rightTree = getDeep(root.right);
  39.     // 判断那里不符合二叉平衡树的要求
  40.     if (Math.abs(leftTree - rightTree) < 2) return root;
  41.     if (leftTree < rightTree) { //左浅 右深 左单旋
  42.         // 获取变化分支的深度
  43.         let changeTree = getDeep(root.right.left)
  44.         // 获取不变分支的深度
  45.         let noChangeTree = getDeep(root.right.right)
  46.         // 当变化分支的深度大于不变化的分支时需要右左双旋
  47.         if (changeTree > noChangeTree) {
  48.             //将右子树进行右单旋
  49.             root.right = rightRotate(root.right)
  50.         }
  51.         // 生成左单旋后的二叉树
  52.         let newRoot =  leftRotate(root)
  53.         // 将其生成后的新二叉树的左子树进行判断
  54.         newRoot.left = change(newRoot.left)
  55.         // 新二叉树的左子树会发生改变，因此将再次判断整个二叉树
  56.         newRoot = change(newRoot)
  57.         return newRoot;
  58.     } else if (leftTree > rightTree) { //左深 右浅 右单旋
  59.         // 获取变化分支的深度
  60.         let changeTree = getDeep(root.left.right)
  61.         // 获取不变分支的深度
  62.         let noChangeTree = getDeep(root.left.left)
  63.         // 当变化分支的深度大于不变化分支的深度将进行左右单旋
  64.         if (changeTree > noChangeTree) {
  65.             // 将其左子树进行左单旋
  66.             root.left = leftRotate(root.left)
  67.         }
  68.         let newRoot =  rightRotate(root);
  69.         // 将其生成后的新二叉树的右子树进行判断
  70.         newRoot.right = change(newRoot.right)
  71.         // 新二叉树的右子树会发生改变，因此将再次判断整个二叉树
  72.         newRoot = change(newRoot)
  73.         return newRoot
  74.     }
  75.     return root
  76. }
  78. /**
  79.  * 判断是否为二叉平衡树
  80.  * 平衡二叉的满足条件
  81.  * 根节点的左子树与右子树的高度差不能超过1
  82.  * 这棵二叉树的每个子树的符合第一条
  83.  * @param {*} root 根节点
  84.  * @returns Boolean
  85.  */
  86. function isBalanceTree(root) {
  87.     if (!root) return true;
  88.     // 获取左右子树的深度
  89.     let left = getDeep(root.left);
  90.     let right = getDeep(root.right);
  91.     // 当左子树与右子树的深度差大于1说明不是二叉平衡树
  92.     if (Math.abs(left - right) > 1) return false;
  93.     // 遍历这个二叉树的每一个子树
  94.     else return isBalanceTree(root.left) && isBalanceTree(root.right);
  97. }
  99. /**
  100.  * 获取二叉树的深度
  101.  * @param {*} root 节点
  102.  * @returns Number 返回左右子树中最深的层数
  103.  */
  104. function getDeep(root) {
  105.     if (!root) return 0;
  106.     let left = getDeep(root.left);
  107.     let right = getDeep(root.right);
  108.     return Math.max(left, right) + 1;
  110. }
  112. /**
  113.  * 左单旋
  114.  * 旋转节点：不平衡的节点为旋转节点
  115.  * 新根：旋转节点的右子树的根节点
  116.  * @param {*} root 旋转节点
  117.  * @returns 新的根节点
  118.  */
  119. function leftRotate(root) {
  120.     // 找到新根
  121.     let newNode = root.right;
  122.     // 找到变化分支
  123.     let changeNode = newNode.left;
  124.     // 当前旋转节点的右孩子为变化分支
  125.     root.right = changeNode;
  126.     // 新根的左孩子为旋转节点
  127.     newNode.left = root;
  128.     // 返回新的根节点
  129.     return newNode;
  131. }
  132. /**
  133.  * 右单旋
  134.  * 旋转节点：不平衡的节点为旋转节点
  135.  * 新根：旋转节点的左子树的根节点
  136.  * @param {*} root 旋转节点
  137.  * @returns 新的根节点
  138.  */
  139. function rightRotate(root) {
  140.     // 找到新根
  141.     let newNode = root.left;
  142.     // 找到变化分支
  143.     let changeNode = newNode.right;
  144.     // 当前旋转节点的左孩子为变化分支
  145.     root.left = changeNode
  146.     // 新根的右孩子为旋转节点
  147.     newNode.right = root;
  148.     // 返回新的根节点
  149.     return newNode;
  151. }
  153. /**
  154.  * 判断是否为平衡二叉树
  155.  * 平衡二叉的满足条件
  156.  * 根节点的左子树与右子树的高度差不能超过1
  157.  * 这棵二叉树的每个子树的符合第一条
  158.  * @param {*} root 节点
  159.  * @returns Boolean
  160.  */
  161. function isBalanceTree(root) {
  162.     if (!root) return true;
  163.     let letTree = getDeep(root.left)
  164.     let rightTree = getDeep(root.right)
  165.     if (Math.abs(letTree - rightTree) > 1) return false
  166.     else return isBalanceTree(root.left) && isBalanceTree(root.right);
  167. }
  168. // 测试右右双旋
  169. let root = change(node9);
  170. console.log(isBalanceTree(root))

红黑树参考资料

参考资料1

网页捕获_20-4-2021_151137_juejin.cn.jpeg

参考资料2

网页捕获_19-4-2021_234427_juejin.cn.jpeg