题目

题目来源：力扣（LeetCode）

在二叉树中，根节点位于深度 0 处，每个深度为 k 的节点的子节点位于深度 k+1 处。
如果二叉树的两个节点深度相同，但 父节点不同 ，则它们是一对堂兄弟节点。

我们给出了具有唯一值的二叉树的根节点 root ，以及树中两个不同节点的值 x 和 y 。

只有与值 x 和 y 对应的节点是堂兄弟节点时，才返回 true 。否则，返回 false。

示例 1：
image.png
输入：root = [1,2,3,4], x = 4, y = 3
输出：false

示例 2：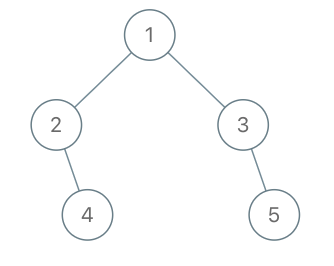
image.png
输入：root = [1,2,3,null,4,null,5], x = 5, y = 4
输出：true

示例 3：
image.png
输入：root = [1,2,3,null,4], x = 2, y = 3
输出：false

思路分析

深度优先搜索

  1. 要想判断两个节点 x 和 y 是否为堂兄弟节点，我们就需要求出这两个节点分别的「深度」以及「父节 点」。
  2. 因此，我们可以从根节点开始，对树进行一次遍历，在遍历的过程中维护「深度」以及「父节点」这 两个信息。
  3. 当我们遍历到 x 或 y 节点时，就将信息记录下来；当这两个节点都遍历完成了以后，我们就可以退出 遍历的过程，判断它们是否为堂兄弟节点了。
  4. 在使用深度优先搜索时，我们只需要在深度优先搜索的递归函数中增加表示「深度」以及「父节点」的两个参数即可。
  1. var isCousins = function (root, x, y) {
  2.   // x_parent x 的父节点
  3.   // x_depth  x 的深度
  4.   // x_found  标记是否找到了 x
  5.   let x_parent = null, x_depth = null, x_found = false;
  6.   // y_parent y 的父节点
  7.   // y_depth  y 的深度
  8.   // y_found  标记是否找到了 y
  9.   let y_parent = null, y_depth = null, y_found = false;
  11.   const dfs = (node, depth, parent) => {
  12.     if (!node) { // 节点为 null 的时候，退出递归函数
  13.       return;
  14.     }
  15.     if (node.val === x) {
  16.       // 找到了 x 节点，把它的父节点和深度记录下来
  17.       [x_parent, x_depth, x_found] = [parent, depth, true];
  18.     } else if (node.val === y) {
  19.       // 找到了 y 节点，把它的父节点和深度记录下来
  20.       [y_parent, y_depth, y_found] = [parent, depth, true];
  21.     }
  23.     // 如果两个节点都找到了，就可以提前退出遍历
  24.     // 即使不提前退出，对最坏情况下的时间复杂度也不会有影响
  25.     if (x_found && y_found) {
  26.       return;
  27.     }
  29.     dfs(node.left, depth + 1, node);
  31.     if (x_found && y_found) {
  32.       return;
  33.     }
  35.     dfs(node.right, depth + 1, node);
  36.   }
  37.   dfs(root, 0, null);
  38.   // 如果确定他俩是堂兄弟节点了，直接返回，不用再往下遍历了
  39.   return x_depth === y_depth && x_parent !== y_parent;
  40. };

广度优先搜索

在广度优先搜索的过程中，每当我们从队首取出一个节点，它就会作为「父节点」，将最多两个子节点放入队尾。因此，除了节点以外，我们只需要在队列中额外存储「深度」的信息即可。

  1. var isCousins = function(root, x, y) {
  2.   // x_parent x 的父节点
  3.   // x_depth  x 的深度
  4.   // x_found  标记是否找到了 x
  5.   let x_parent = null, x_depth = null, x_found = false;
  6.   // y_parent y 的父节点
  7.   // y_depth  y 的深度
  8.   // y_found  标记是否找到了 y
  9.   let y_parent = null, y_depth = null, y_found = false;
  11.   // 用来判断是否遍历到 x 或 y 的辅助函数
  12.   const update = (node, parent, depth) => {
  13.     if (node.val === x) {
  14.       // 找到了 x 节点，把它的父节点和深度记录下来
  15.       [x_parent, x_depth, x_found] = [parent, depth, true];
  16.     } else if (node.val === y) {
  17.       // 找到了 y 节点，把它的父节点和深度记录下来
  18.       [y_parent, y_depth, y_found] = [parent, depth, true];
  19.     }
  20.   }
  22.   // 队列存储节点及深度
  23.   let q = [[root, 0]];
  24.   update(root, null, 0);
  26.   while (q.length) {
  27.     // 从队列中拿出一个节点，
  28.     const [node, depth] = q.shift()
  29.     if (node.left){
  30.       q.push([node.left, depth + 1]);
  31.       update(node.left, node, depth + 1);
  32.     }
  33.     if (node.right) {
  34.       q.push([node.right, depth + 1]);
  35.       update(node.right, node, depth + 1);
  36.     }
  38.     if (x_found && y_found) {
  39.         break;
  40.     }
  41.   }
  43.   // 如果确定他俩是堂兄弟节点了，直接返回，不用再往下遍历了
  44.   return x_depth === y_depth && x_parent !== y_parent;
  45. };