栈和队列的介绍

栈和队列是两种重要的线性结构，从数据结构角度看，栈和队列也是线性表，其特殊性在与栈和队列的基本操作是线性表操作的子集，它们是受限制的线性表，因此可称为限定性数据结构，但从数据类型角度看，它们是和线性表大不相同的两类重要的抽象数据类型。
队列和栈都可以使用顺序线性表和链线性表的方式实现

栈

是限定仅在表尾进行插入或删除操作的线性表。因此，对栈来说，表尾端有其特殊的含义，称为“栈顶”，相应的表头端称为“栈底”。不含元素的空表叫做“空栈”，栈又叫做先进后出的线性表。

  • InitStack(&S); // 初始化栈
  • DestroyStack(&S); // 销毁栈
  • ClearStack(&S); // 清空栈
  • StackEmpty(&S); // 检测是不是空栈，若为空返回TRUE，不为空返回FALSE
  • StackLength(&S); // 返回栈的长度
  • StackGetTop(&S, &e); // 返回栈顶元素
  • StackPush(&S, &e); // 向栈顶插入元素
  • StackPop(&S, &e); // 删除栈顶元素，并通过e返回
  • StackTraverse(&S, visit()); // 栈中所有元素依次调用visit()。一旦visit()失败，则操作失败

和线性表一样，栈也有两种存储表示方式（顺序栈，先给个默认长度，然后在给一个递增长度，递增类型的）

  1. #include <stdio.h>
  2. #include <stdlib.h>
  3. #define TRUE 1
  4. #define FALSE 0
  5. #define ERROR 0
  6. #define OK 1
  7. #define OVERFLOW -2
  8. #define STACK_INIT_SIZE 100
  9. #define STACKINCREMENT 10
  10. typedef int ElemType;
  11. typedef int Status;
  12. typedef struct {
  13.     ElemType *base; // 栈底
  14.   ElemType *top; // 栈顶
  15.   int stacksize;
  16. }SqStack;
  18. Status InitStack(SqStack *S) {
  19.     S -> base = (ElemType *)malloc(STACK_INIT_SIZE * sizeof(ElemType));
  20.     if (!S-> base) {
  21.         exit(OVERFLOW);
  22.     }
  23.     S -> top = S -> base;
  24.     S -> stacksize = STACK_INIT_SIZE;
  25.     return OK;
  26. }
  28. Status StackGetTop(SqStack *S, ElemType *e) {
  29.     if (S -> top == S -> base) {
  30.         return ERROR;
  31.     }
  32.     *e = *(S -> top -1);
  33.     return OK;
  34. }
  36. Status StackPush(SqStack *S, ElemType e) {
  37.     if (S -> top - S -> base >= S -> stacksize) {
  38.         S -> base = (ElemType *)realloc(S -> base, 
  39.                     (S -> stacksize + STACKINCREMENT) * sizeof(ElemType));
  40.         if (!S -> base) {
  41.             exit(OVERFLOW);
  42.         }
  43.         S -> top = S -> base + S -> stacksize;
  44.         S -> stacksize += STACKINCREMENT;
  45.     }
  46.     *S -> top++ = e;
  47.     return OK;
  48. }
  50. Status StackPop(SqStack *S, ElemType *e) {
  51.   if (S -> top == S -> base ) {
  52.     return ERROR;
  53.   }
  54.   *e = *--S -> top;
  55.   return OK;
  56. }
  58. Status StackEmpty(SqStack *S) {
  59.   Status z = S -> top == S -> base ? TRUE : FALSE;
  60.   return z;
  61. }
  63. int main() {
  64.   SqStack S;
  65.   InitStack(&S);
  66.   // ElemType e = 2;
  67.   // ElemType v;
  68.   // StackPush(&S, e);
  69.   // StackPop(&S, &v);
  70.   // StackGetTop(&S, &v);
  71.   // printf("d=%d\n", v);
  72.   int n;
  73.   ElemType e;
  74.   scanf("%d", &n);
  75.   while (n) {
  76.     StackPush(&S, n % 8);
  77.     n /= 8;
  78.   }
  80.   while(!StackEmpty(&S)) {
  81.     StackPop(&S, &e);
  82.     printf("%d", e);
  83.   }
  84.   printf("\n");
  85.   return 0;
  86. }

栈的应用实例

数制转换

（1348）十进制 = (2504) 八进制
1348 % 8 = 4
1348 ／ 8 = 168; 168 % 8 = 0;
168 / 8 = 21; 21 % 8 = 5;
21 / 8 = 2; 2 % 8 = 2;

  1. int main() {
  2.   SqStack S;
  3.   InitStack(&S);
  4.   int n;
  5.   ElemType e;
  6.   scanf("%d", &n);
  7.   while (n) {
  8.     StackPush(&S, n % 8);
  9.     n /= 8;
  10.   }
  11.   while(!StackEmpty(&S)) {
  12.     StackPop(&S, &e);
  13.     printf("%d", e);
  14.   }
  15.   printf("\n");
  16.   return 0;
  17. }

行编辑程序

  1. #include <stdio.h>
  2. #include <stdlib.h>
  3. #define TRUE 1
  4. #define FALSE 0
  5. #define ERROR 0
  6. #define OK 1
  7. #define OVERFLOW -2
  8. #define STACK_INIT_SIZE 100
  9. #define STACKINCREMENT 10
  10. typedef char ElemType;
  11. typedef char Status;
  12. typedef struct {
  13.     ElemType *base; // 栈底
  14.   ElemType *top; // 栈顶
  15.   int stacksize;
  16. }SqStack;
  18. Status InitStack(SqStack *S) {
  19.     S -> base = (ElemType *)malloc(STACK_INIT_SIZE * sizeof(ElemType));
  20.     if (!S-> base) {
  21.         exit(OVERFLOW);
  22.     }
  23.     S -> top = S -> base;
  24.     S -> stacksize = STACK_INIT_SIZE;
  25.     return OK;
  26. }
  28. Status StackGetTop(SqStack *S, ElemType *e) {
  29.     if (S -> top == S -> base) {
  30.         return ERROR;
  31.     }
  32.     *e = *(S -> top -1);
  33.     return OK;
  34. }
  36. Status StackPush(SqStack *S, ElemType e) {
  37.     if (S -> top - S -> base >= S -> stacksize) {
  38.         S -> base = (ElemType *)realloc(S -> base, 
  39.                     (S -> stacksize + STACKINCREMENT) * sizeof(ElemType));
  40.         if (!S -> base) {
  41.             exit(OVERFLOW);
  42.         }
  43.         S -> top = S -> base + S -> stacksize;
  44.         S -> stacksize += STACKINCREMENT;
  45.     }
  46.     *S -> top++ = e;
  47.     return OK;
  48. }
  50. Status StackPop(SqStack *S, ElemType *e) {
  51.   if (S -> top == S -> base ) {
  52.     return ERROR;
  53.   }
  54.   *e = *--S -> top;
  55.   return OK;
  56. }
  58. Status ClearStack(SqStack *S) {
  59.   S -> top = S -> base; 
  60.   return OK;
  61. }
  63. Status StackEmpty(SqStack *S) {
  64.   Status z = S -> top == S -> base ? TRUE : FALSE;
  65.   return z;
  66. }
  68. void LineEdit(SqStack *S) {
  69.   printf("请输入字符:\n");
  70.   InitStack(S);
  71.   char ch; 
  72.   scanf("%c", &ch);
  73.   while ((int)ch != 27) {
  74.     switch(ch) {
  75.       case '#': 
  76.         StackPop(S, &ch);
  77.         break;
  78.       case '@': // 期待删除 \n?.*@.*\n 之间的内容
  79.         ClearStack(S);
  80.         break;
  81.       default: StackPush(S, ch);
  82.     }
  83.     scanf("%c", &ch);
  84.     if (ch == '\n') {
  85.       StackPush(S, ch);
  86.       scanf("%c", &ch);
  87.     }
  88.   }
  89. }
  91. int main() {
  92.   SqStack S;
  93.   LineEdit(&S);
  94.   char e;
  95.   while(!StackEmpty(&S)) {
  96.     StackPop(&S, &e);
  97.     printf("%c", e);
  98.   }
  99.   printf("\n");
  100.   return 0;
  101. }

括号匹配的检测

{[][]{}}

  1. #include <stdio.h>
  2. #include <stdlib.h>
  3. #define TRUE 1
  4. #define FALSE 0
  5. #define ERROR 0
  6. #define NO 0
  7. #define OK 1
  8. #define OVERFLOW -2
  9. #define STACK_INIT_SIZE 100
  10. #define STACKINCREMENT 10
  11. typedef char ElemType;
  12. typedef char Status;
  13. typedef struct {
  14.     ElemType *base; // 栈底
  15.   ElemType *top; // 栈顶
  16.   int stacksize;
  17. }SqStack;
  19. Status InitStack(SqStack *S) {
  20.     S -> base = (ElemType *)malloc(STACK_INIT_SIZE * sizeof(ElemType));
  21.     if (!S-> base) {
  22.         exit(OVERFLOW);
  23.     }
  24.     S -> top = S -> base;
  25.     S -> stacksize = STACK_INIT_SIZE;
  26.     return OK;
  27. }
  29. Status StackGetTop(SqStack *S, ElemType *e) {
  30.     if (S -> top == S -> base) {
  31.         return ERROR;
  32.     }
  33.     *e = *(S -> top -1);
  34.     return OK;
  35. }
  37. Status StackPush(SqStack *S, ElemType e) {
  38.     if (S -> top - S -> base >= S -> stacksize) {
  39.         S -> base = (ElemType *)realloc(S -> base, 
  40.                     (S -> stacksize + STACKINCREMENT) * sizeof(ElemType));
  41.         if (!S -> base) {
  42.             exit(OVERFLOW);
  43.         }
  44.         S -> top = S -> base + S -> stacksize;
  45.         S -> stacksize += STACKINCREMENT;
  46.     }
  47.     *S -> top++ = e;
  48.     return OK;
  49. }
  51. Status StackPop(SqStack *S, ElemType *e) {
  52.   if (S -> top == S -> base) {
  53.     return ERROR;
  54.   }
  55.   *e = *--S -> top;
  56.   return OK;
  57. }
  59. Status ClearStack(SqStack *S) {
  60.   S -> top = S -> base; 
  61.   return OK;
  62. }
  64. Status StackEmpty(SqStack *S) {
  65.   Status z = S -> top == S -> base ? TRUE : FALSE;
  66.   return z;
  67. }
  69. Status Match(char a,char b){  
  70.   if (a + 1 == b || a + 2 == b) {
  71.     return OK;
  72.   }   
  73.   return NO;  
  74. } 
  76. Status BracketsMatching(char *str) {
  77.   SqStack S;
  78.   InitStack(&S);
  79.   int i;
  80.   char ch;
  81.   for (i = 0; str[i] != '\0'; i++) {
  82.     switch (str[i]) {
  83.       case '{': 
  84.       case '(': 
  85.       case '[':
  86.         StackPush(&S, str[i]); 
  87.         break;
  88.       case '}':
  89.       case ')': 
  90.       case ']': 
  91.         if (StackEmpty(&S)){    
  92.           return NO;  
  93.         }  
  94.         StackGetTop(&S, &ch);
  95.         if (Match(ch, str[i])) {
  96.           StackPop(&S, &ch);
  97.         } else {
  98.           return NO;
  99.         }
  100.         break;
  101.       default: 
  102.       break;
  103.     }
  104.   }
  105.   if (!StackEmpty(&S)) {
  106.     return NO;
  107.   }
  108.   return OK;
  109. }
  111. int main() {
  112.   Status StackEmpty(SqStack *S);
  113.   Status StackPush(SqStack *S, ElemType e);
  114.   Status StackPop(SqStack *S, ElemType *e);
  116.   char str[50];
  117.   printf("请输入你要收入的字符串：");
  118.   scanf("%s", str);
  119.   int h = BracketsMatching(str);
  120.   if(h == 0)
  121.       printf("括号不匹配\n");
  122.   else
  123.       printf("括号匹配\n");
  124.   return 0;
  125. }

迷宫求解

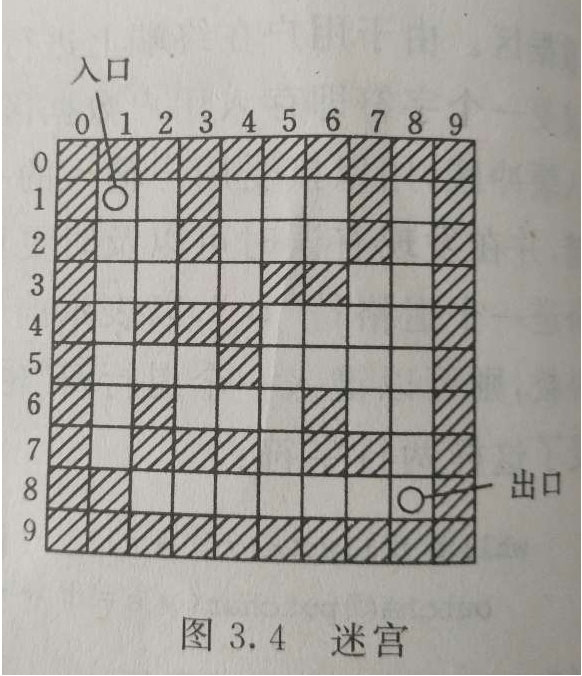
求迷宫从入口到出口的所有路径是一个经典的程序设计问题。由于计算机解迷宫时，通常用的是“穷举求解”的方法，即从入口出发，顺某一个方向向前探索，若能走通，则继续向前，否则按原路退回，换一个方向继续探索，直至所有可能的路线都探索到了为止。为了保证在任何位置上都能按原路退回，显然需要用一个后进先出的结构来保存从入口到当前位置的路径。因此求解迷宫通路的算法中应用“栈”也就是自然而然的事情了。
首先，在计算机中可以用如图所示的方块图表示迷宫。图中空白处可以通行，阴影处表示是墙壁。所求路径必须是简单路径，即在求得路径上不能重复出现同一通道块。
假设“当前位置”指的是“在搜索过程中某一时刻所在图中某个方块的位置”，则求迷宫中一条路径的算法的基本思想是：
若当前位置“可通”，则纳入“当前路径”，并继续朝下一个位置探索，即切换“下一位置”为当前位置，如此反复直至到达出口；若当前位置“不可通”，则顺应“来向”退回到前一块通道，然后朝则除“来向”之外的其他地方探索；若该通道块的四周四个方块均不可通，则应顺从“当前路径”上删除该通道块。所谓“下一位置”指的是当前位置的四周4个方向（上，下，左，右）上相邻的方块。
假设栈S纪录当前路径，则栈顶中存放的是“当前路径上最后一个通道块”。由此“纳入路径”的操作即为“当前位置入栈“，“从当前路径上最后一个通道块”的操作即为“出栈”。

IMG_20190708_111943.jpg

  1. #include <stdio.h>
  2. #include <stdlib.h>
  3. #define TRUE 1
  4. #define FALSE 0
  5. #define ERROR 0
  6. #define NO 0
  7. #define OK 1
  8. #define OVERFLOW -2
  9. #define STACK_INIT_SIZE 100
  10. #define STACKINCREMENT 10
  12. typedef struct{
  13.   int x;
  14.   int y;
  15. }PosType;
  17. typedef struct{
  18.   int ord; // 通道块在路径上的“序号”
  19.   PosType seat; // 通道块在迷宫中的坐标位置
  20.   int di; // 通道块走向下一通道块的方向 1上， 2右，3下，4左
  21. }MazeElemType;
  23. typedef struct {
  24.   int rowsLength; // 行长度
  25.   int columnLength; // 列长度
  26.   int *mazeArr; // 地图数组
  27. }MazeType;
  29. typedef MazeElemType ElemType;
  30. typedef int Status;
  32. #define StatusPrintf "%d\n"
  34. typedef struct {
  35.     ElemType *base; // 栈底
  36.   ElemType *top; // 栈顶
  37.   int stacksize;
  38. }SqStack;
  41. Status InitStack(SqStack *S) {
  42.     S -> base = (ElemType *)malloc(STACK_INIT_SIZE * sizeof(ElemType));
  43.     if (!S-> base) {
  44.         exit(OVERFLOW);
  45.     }
  46.     S -> top = S -> base;
  47.     S -> stacksize = STACK_INIT_SIZE;
  48.     return OK;
  49. }
  51. Status StackGetTop(SqStack *S, ElemType *e) {
  52.     if (S -> top == S -> base) {
  53.         return ERROR;
  54.     }
  55.     *e = *(S -> top -1);
  56.     return OK;
  57. }
  59. Status StackPush(SqStack *S, ElemType e) {
  60.     if (S -> top - S -> base >= S -> stacksize) {
  61.         S -> base = (ElemType *)realloc(S -> base, 
  62.                     (S -> stacksize + STACKINCREMENT) * sizeof(ElemType));
  63.         if (!S -> base) {
  64.             exit(OVERFLOW);
  65.         }
  66.         S -> top = S -> base + S -> stacksize;
  67.         S -> stacksize += STACKINCREMENT;
  68.     }
  69.     *S -> top++ = e;
  70.     return OK;
  71. }
  73. Status StackPop(SqStack *S, ElemType *e) {
  74.   if (S -> top == S -> base) {
  75.     return ERROR;
  76.   }
  77.   *e = *--S -> top;
  78.   return OK;
  79. }
  81. Status ClearStack(SqStack *S) {
  82.   S -> top = S -> base; 
  83.   return OK;
  84. }
  86. Status StackEmpty(SqStack *S) {
  87.   Status z = S -> top == S -> base ? TRUE : FALSE;
  88.   return z;
  89. }
  92. PosType NextPos(PosType curpos, int di) {
  93.   switch(di) {
  94.     case 1: 
  95.       curpos.x -= 1; 
  96.     break;
  97.     case 2: 
  98.       curpos.y += 1;
  99.     break;
  100.     case 3: 
  101.       curpos.x += 1;
  102.     break;
  103.     case 4:
  104.       curpos.y -= 1; 
  105.     break;
  106.     default:
  107.     break;
  108.   }
  109.   int i = 0;
  110.   int num = 0;
  111.   for (; i < 1000000; i += 1) {
  112.     num = i;
  113.   }
  114.   return curpos;
  115. }
  117. Status Pass(MazeType *maze, PosType curpos) { // 是否可通行块
  118.   if (curpos.x > maze -> rowsLength 
  119.   || curpos.y > maze -> columnLength
  120.   || curpos.x < 0
  121.   || curpos.y < 0) {
  122.     return FALSE;
  123.   }
  124.   int *p = maze -> mazeArr;
  125.   int q = *(p + curpos.x * 10 + curpos.y);
  126.   Status z = q > 0 ? TRUE : FALSE;
  127.   return z;
  128. }
  130. Status MarkPrint(MazeType *maze, PosType curpos) { // 标记地图不能行走
  131.   int *p = maze -> mazeArr;
  132.   *(p + curpos.x * 10 + curpos.y) = 0;
  133.   return OK;
  134. }
  136. Status TheWayThrough(SqStack *S, PosType temp) { // 判断是否存在链表中
  137.   SqStack Temp;
  138.   InitStack(&Temp);
  139.   Status z = FALSE;
  140.   MazeElemType e;
  141.   while(!StackEmpty(S)) {
  142.     StackPop(S, &e);
  143.     StackPush(&Temp, e);
  144.     if (e.seat.x == temp.x && e.seat.y == temp.y) {
  145.       z = TRUE;
  146.     }
  147.   }
  148.   while(!StackEmpty(&Temp)) {
  149.     StackPop(&Temp, &e);
  150.     StackPush(S, e);
  151.   }
  152.   return z;
  153. }
  155. /*
  156.   如果下个位置存在与链表中，跳过此次
  157. */
  158. Status CurposNext(MazeType *maze, SqStack *S, PosType *curpos, MazeElemType *e) {
  159.   while (TheWayThrough(S, *curpos)) {
  160.     if (e -> di == 4) {
  161.       MarkPrint(maze, *curpos);
  162.       StackPop(S, e);
  163.       printf("F pop:%d:%d di=%d\n", e -> seat.x, e -> seat.y, e -> di);
  164.     } else {
  165.       StackPop(S, e);
  166.       e -> di += 1;
  167.       StackPush(S, *e);
  168.       printf("E :%d:%d di=%d\n", e -> seat.x, e -> seat.y, e -> di);
  169.       *curpos = NextPos(e -> seat, e -> di);
  170.     }
  171.   }
  172.   return OK;
  173. }
  175. Status MazePath(MazeType *maze, PosType start, PosType end) {
  176.   SqStack S;
  177.   InitStack(&S);
  178.   PosType curpos = start; // 设置起始位置 8,8
  179.   int curstep = 1; // 第一步
  180.   MazeElemType e;
  181.   int i;
  182.   do {
  183.     i++;
  184.     Status z = Pass(maze, curpos); // 是否可通行块
  185.     if (z) { // 当前位置是可通行块
  186.       e.ord = curstep;
  187.       e.seat = curpos;
  188.       e.di = 1; // 通过di留下足迹
  189.       StackPush(&S, e);
  190.       printf("A push:%d:%d di=%d\n", e.seat.x, e.seat.y, e.di);
  191.       if (curpos.x == end.x
  192.       && curpos.y == end.y) {
  193.         printf("i=%d\n", i);
  194.         return OK;
  195.       }
  196.       curpos = NextPos(curpos, 1); // 下一个位置
  197.       CurposNext(maze, &S, &curpos, &e);
  198.       curstep++;
  199.     } else { // 当前位置为不可通行块
  200.       if (!StackEmpty(&S)) {
  201.         StackPop(&S, &e);
  202.         printf("B pop:%d:%d di=%d\n", e.seat.x, e.seat.y, e.di);
  203.         while(e.di == 4 && !StackEmpty(&S)) {
  204.           // 标记地图不可通行
  205.           MarkPrint(maze, curpos);
  206.           StackPop(&S, &e);
  207.           printf("D MarkPrint pop:%d:%d di=%d\n", e.seat.x, e.seat.y, e.di);
  208.           curpos = e.seat;
  209.         }
  210.         if (e.di < 4) {
  211.           e.di += 1;
  212.           StackPush(&S, e);
  213.           printf("C push:%d:%d di=%d\n", e.seat.x, e.seat.y, e.di);
  214.           curpos = NextPos(e.seat, e.di);
  215.           CurposNext(maze, &S, &curpos, &e);
  216.         }
  217.       }
  218.     }
  220.   } while (!StackEmpty(&S));
  221.   printf("i=%d\n", i);
  222.   return FALSE;
  223. }
  225. int main() {
  226.   Status StackEmpty(SqStack *S);
  227.   Status StackPush(SqStack *S, ElemType e);
  228.   Status StackPop(SqStack *S, ElemType *e);
  229.   Status MarkPrint(MazeType *maze, PosType curpos);
  230.   PosType NextPos(PosType curpos, int di);
  231.   Status Pass(MazeType *maze, PosType curpos);
  232.   Status MazePath(MazeType *maze, PosType start, PosType end);
  233.   Status TheWayThrough(SqStack *S, PosType temp);
  234.   Status CurposNext(MazeType *maze, SqStack *S, PosType *curpos, MazeElemType *e);
  236.   int Maze[10][10] = { // 迷宫  2为出口，3为入口，1为可通行块，0为不可通行块
  237.     { 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 },
  238.     { 0, 2, 1, 0, 1, 1, 1, 0, 1, 0 },
  239.     { 0, 1, 1, 0, 1, 1, 1, 0, 1, 0 },
  240.     { 0, 1, 1, 1, 1, 0, 0, 1, 1, 0 },
  241.     { 0, 1, 0, 0, 0, 1, 1, 1, 1, 0 },
  242.     { 0, 1, 1, 1, 0, 1, 1, 1, 1, 0 },
  243.     { 0, 1, 0, 1, 1, 1, 0, 1, 1, 0 },
  244.     { 0, 1, 0, 0, 0, 1, 0, 0, 1, 0 },
  245.     { 0, 0, 1, 1, 1, 1, 1, 1, 3, 0 },
  246.     { 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 },
  247.   };
  249.   int *p = &Maze[0][0];
  250.   MazeType maze = { 10, 10, p };
  251.   PosType start = { 8, 8 };
  252.   PosType end = { 1, 1 };
  253.   int i = MazePath(&maze, start, end);
  254.   if (i == 0) {
  255.     printf("没有找到出口\n");
  256.   } else {
  257.     printf("找到出口了\n");
  258.   }
  259.   return 0;
  260. }

表达式求值

  1. #include <stdio.h>
  2. #include <stdlib.h>
  4. #define TRUE 1
  5. #define FALSE 0
  6. #define OK 1
  7. #define ERROR 0
  8. #define INFEASIBLE -1  
  9. #define OVERFLOW -2
  10. #define STACK_INIT_SIZE 100   //存储空间初始分配量
  11. #define STACKINCREMENT 10   //存储空间分配增量
  13. typedef char SElemType;
  14. typedef char OperandType;   //表达式求值的运算类型
  15. typedef int Status;
  17. typedef struct
  18. {
  19.     SElemType *base;
  20.     SElemType *top;
  21.     int stacksize;
  22. }SqStack;
  24. //构造一个空栈
  25. Status InitStack(SqStack *S)
  26. {
  27.     S->base = (SElemType *)malloc(STACK_INIT_SIZE * sizeof(SElemType));
  28.     if(!S->base)
  29.     {
  30.         printf("内存分配失败!\n");
  31.         exit(OVERFLOW);
  32.     }
  34.     S->top = S->base;
  35.     S->stacksize = STACKINCREMENT;
  36.     return OK;
  37. }
  39. //若栈不为空，则用e返回S的栈顶元素，并返回OK；否则返回ERROR
  40. Status GetTop(SqStack *S, SElemType *e)
  41. {
  42.     if(S->top == S->base)
  43.         return ERROR;
  45.     *e = *(S->top - 1);
  46.     return OK;
  47. }
  49. //插入元素e为新的栈顶元素
  50. Status Push(SqStack *S, SElemType e)
  51. {
  52.     if(S->top - S->base >= STACK_INIT_SIZE)   //栈满， 追加存储空间
  53.     {
  54.         S->base = (SElemType *)realloc(S->base, (S->stacksize + STACKINCREMENT) * sizeof(SElemType));
  55.         if(!S->base)
  56.         {
  57.             printf("内存分配失败!\n");
  58.             exit(OVERFLOW);
  59.         }
  61.         S->top = S->base + S->stacksize;
  62.         S->stacksize += STACKINCREMENT;
  63.     }
  65.     *S->top++ = e;
  67.     return OK;
  68. }
  70. //若栈不为空，则删除S的栈顶元素，用e返回其值，并返回Ok；否则返回ERROR
  71. Status Pop(SqStack *S, SElemType *e)
  72. {
  73.     if(S->top == S->base)
  74.         return ERROR;
  76.     *e =  *--S->top;
  78.     return OK;
  79. }
  80. //销毁栈S，使其不复存在
  81. Status StackDestroy(SqStack *S)
  82. {
  83.     free(S->base);
  84.     S->base = NULL;
  85.     S->top = NULL;
  86.     S->stacksize = 0;
  87.     return OK;
  88. }
  90. //清空栈S，保留栈底指针
  91. void ClearStack(SqStack *S)
  92. {
  93.     S->top = S->base;
  94. }
  96. //根据教科书表3.1，判断两符号的优先关系
  97. char Precede(char t1, char t2){  
  98.     int i,j;  
  99.     char pre[][7]={           
  100.     //运算符之间的优先级制作成一张表格  
  101.         {'>','>','<','<','<','>','>'},  
  102.         {'>','>','<','<','<','>','>'},  
  103.         {'>','>','>','>','<','>','>'},  
  104.         {'>','>','>','>','<','>','>'},  
  105.         {'<','<','<','<','<','=','0'},  
  106.         {'>','>','>','>','0','>','>'},  
  107.         {'<','<','<','<','<','0','='}};  
  108.     switch(t1){  
  109.         case '+': i=0; break;  
  110.         case '-': i=1; break;  
  111.         case '*': i=2; break;  
  112.         case '/': i=3; break;  
  113.         case '(': i=4; break;  
  114.         case ')': i=5; break;  
  115.         case '=': i=6; break;  
  116.     }  
  117.     switch(t2){  
  118.         case '+': j=0; break;  
  119.         case '-': j=1; break;  
  120.         case '*': j=2; break;  
  121.         case '/': j=3; break;  
  122.         case '(': j=4; break;  
  123.         case ')': j=5; break;  
  124.         case '=': j=6; break;  
  125.     }  
  126.     return pre[i][j];  
  127. }  
  128. //判断c是否为运算符
  129. Status In(OperandType c)
  130. {
  131.     switch(c)
  132.     {
  133.     case '+':
  134.     case '-':
  135.     case '*':
  136.     case '/':
  137.     case '(':
  138.     case ')':
  139.     case '=':
  140.         return TRUE;
  141.     default:
  142.         return FALSE;
  143.     }
  145. }
  147. //二元运算(a theta b)
  148. OperandType Operate(OperandType a, OperandType theta, OperandType b)
  149. {
  150.     OperandType c;
  151.     switch(theta)
  152.     {
  153.     case '+':
  154.         c = a + b;
  155.         break;
  156.     case '-':
  157.         c = a - b;
  158.         break;
  159.     case '*':
  160.         c = a * b;
  161.         break;
  162.     case '/':
  163.         c = a / b;
  164.         break;
  165.     }
  166.     return c;
  167. }
  169. //算术表达式求值的算符优先算法，设OPTR和OPND分别为运算符栈和运算数栈，OP为运算符集合
  170. OperandType EvaluateExpression()
  171. {
  172.     SqStack OPTR, OPND;
  173.     OperandType a, b, d, x, theta;
  174.     char c;   //存放有键盘输入的字符串
  175.     char z[6];   //存放整数字符串
  176.     int i;
  177.     InitStack(&OPTR);   //初始化运算符栈
  178.     Push(&OPTR, '=');   //=是表达式结束符
  179.     InitStack(&OPND);   //初始化运算数栈
  181.     c = getchar();
  182.     GetTop(&OPTR, &x);
  183.     while(c != '=' || x != '=')
  184.     {
  185.         if(In(c))   //是7种运算符之一
  186.         {
  187.       printf("%c\n", Precede(x, c));
  188.             switch(Precede(x, c))
  189.             {
  190.             case '<':   //当前已经压栈一个运算符（x）比后一个运算符（c）低时，就将c压栈
  191.                 Push(&OPTR, c);
  192.                 c = getchar();
  193.                 break;
  194.             case '=':
  195.                 Pop(&OPTR, &x);   //脱括号并接收下一字符
  196.                 c = getchar();
  197.                 break;
  198.             case '>':
  199.                 Pop(&OPTR, &theta);   //退栈并将运算结果压入OPND中
  200.                 Pop(&OPND, &b);
  201.                 Pop(&OPND, &a);
  202.                 Push(&OPND, Operate(a, theta, b));
  203.                 break;
  204.             }
  205.         }
  206.             else if(c >= '0' && c <= '9')   //c是操作数
  207.             {
  208.                 i = 0;
  209.                 do
  210.                 {
  211.                     z[i] = c;
  212.                     i++;
  213.                     c = getchar();
  214.                 }while(c >= '0' && c <= '9');
  215.                 z[i] = 0;
  216.                 d = atoi(z);   //将字符数组转为整型存于d
  217.         printf("%d\n", d);
  218.                 Push(&OPND, d);
  219.             }
  220.             else   //c为非法字符
  221.             {
  222.                 printf("ERROR3\n");
  223.                 exit(1);
  224.             }
  225.             GetTop(&OPTR, &x);
  226.         }
  227.     GetTop(&OPND, &x);
  228.     StackDestroy(&OPTR);
  229.     StackDestroy(&OPND);
  230.     return x;
  231. }
  233. int main()
  234. {
  235.     printf("请输入算术表达式，负数要用（0-正数:\n");
  236.     printf("%d\n", EvaluateExpression());
  237.     return 0;
  238. }

栈和递归 hanoi塔

  1. #include <stdio.h>
  3. int c = 0;
  4. void move(char a,int m,char b);
  5. void hanoi(int n,char x,char y,char z);
  6. int main()
  7. {
  8.     int n = 4;
  9.     char x = 'x';
  10.     char y = 'y';
  11.     char z = 'z';
  12.     hanoi(n,x,y,z);
  13. }
  15. void hanoi(int n,char x,char y,char z)
  16. //将塔座x上按直径由小到大且自上而下编号为1至n的n个圆盘按规则搬到
  17. //塔座z上，y可用辅助塔座。
  18. {
  19.     if(n==1)
  20.         move(x,1,z);
  21.     else
  22.     {
  23.         hanoi(n-1,x,z,y);
  24.         move(x,n,z);
  25.         hanoi(n-1,y,x,z);
  26.     }
  27. }
  29. void move(char a,int m,char b)
  30. {
  31.     printf("第%d步:将第%d个圆盘从%c移到%c\n",++c,m,a,b);
  32. }

队列

  • 和栈相反队列是一种先进先出的线性表，也是利用线性表的实现
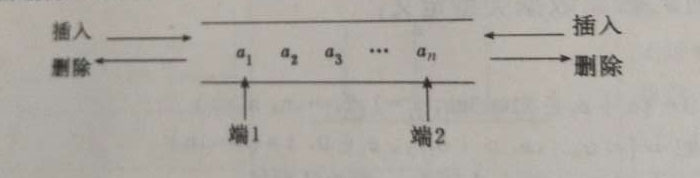
  • 有一种队列叫做，双端队列，两头都可以删除和插入，分为端点1，端点2

IMG_20190710_171103.jpg

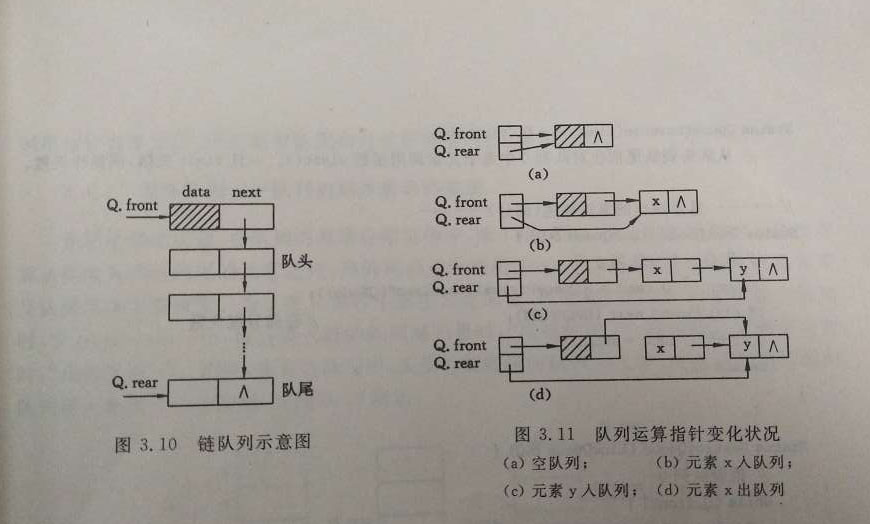
链队列

  1. #include <stdio.h>
  2. #include <stdlib.h>
  3. #define TRUE 1
  4. #define FALSE 0
  5. #define ERROR 0
  6. #define NO 0
  7. #define OK 1
  8. #define OVERFLOW -2
  9. #define STACK_INIT_SIZE 100
  10. #define STACKINCREMENT 10
  11. typedef int QElemType;
  12. typedef int Status;
  13. typedef struct QNode{
  14.     QElemType data;
  15.     struct QNode *next;
  16. }QNode, *QueuePtr;
  18. typedef struct {
  19.     QueuePtr front; // 对头指针
  20.     QueuePtr rear; // 队尾指针
  21. }LinkQueue;
  23. Status InitQueue(LinkQueue *Q) {
  24.     Q -> front = Q -> rear = (QueuePtr)malloc(sizeof(QNode));
  25.     if (!Q-> front) {
  26.         exit(OVERFLOW);
  27.     }
  28.     Q -> front = NULL;
  29.     return OK;
  30. }
  32. Status EnQueue(LinkQueue *Q, QElemType e) {
  33.     QueuePtr p = (QueuePtr)malloc(sizeof(QNode));
  34.     if (!p) {
  35.         exit(OVERFLOW);
  36.     }
  37.     p -> data = e;
  38.     p -> next = NULL;
  39.     Q -> rear -> next = p;
  40.     Q -> rear = p;
  41.     return OK;
  42. }
  44. Status DeQueue(LinkQueue *Q, QElemType *e) {
  45.     if (Q -> front == Q -> rear) {
  46.         return ERROR;
  47.     }
  48.     QueuePtr p = Q -> front -> next;
  49.     *e = p -> data;
  50.     Q -> front -> next = p -> next;
  51.     if (Q -> rear == p) {
  52.         Q -> rear = Q -> front;
  53.     }
  54.     free(p);
  55.     return OK;
  56. }
  58. int main () {
  59.     return 0;
  60. }

IMG_20190710_164105.jpg

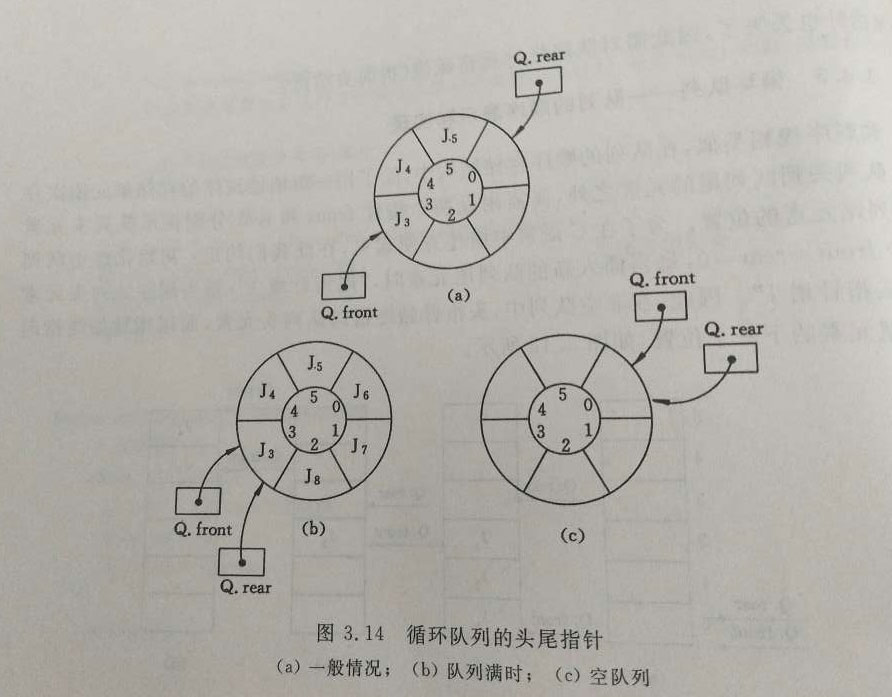
循环队列—队列的顺序表示

  • 假设当前队列分配的最大空间为6，填满，然后出队列4个，还剩2个位置时，不能在继续向队尾插入新元素，否则会因数组越界而导致程序代码被破坏。然而此时又不宜如顺序栈哪样，进行存储在分配扩大数组空间，因为队列的实际可用空间未被占满，一个巧妙的办法是将顺序队列臆造为一个环形的空间。

IMG_20190710_171051.jpg