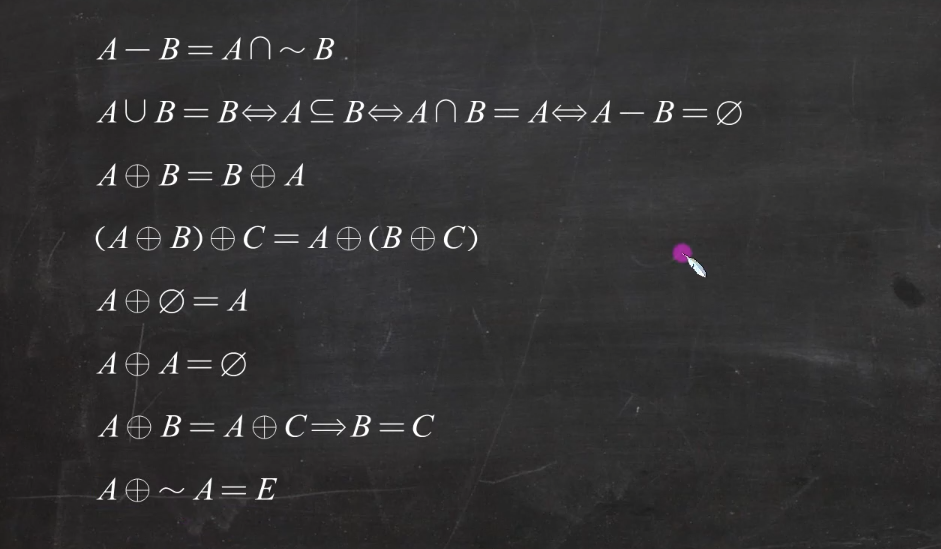1、集合的基本概念

• 集合：把一些事物汇集在一起组成一个整体，就称为是集合。这些事物就是这个集合中的元素或者成员。元素和集合之间的关系是隶属关系，即只有属于或不属于，属于记作，不属于记作
• 子集：设A,B是两个集合，如果B中的每一个元素在A中都能够找到，那么就称B是A的子集，记作
• 相等：如果，那么就称A和B是相等的，记作
• 真子集：如果，那么就称B是A的真子集
• 空集：不包含任何元素的集合称之为空集，空集是一切集合的子集
• n元集：含有n个元素的集合称为是n元集，它的含有m(m<=n)个元素的子集称作它的m元子集

例题：对集合A的子集分类

幂集：设A是一个集合，将A的全体子集构成的集合我们称为A的幂集，记作P(A)

如果A是n元集，那么P(A)就有个元素（一个集合有个子集）

全集：在一个具体的问题中，如果所涉及到的集合都是某个集合的子集，那么就称这个集合为全集，记作E

例题：集合的基本概念

2、集合的运算

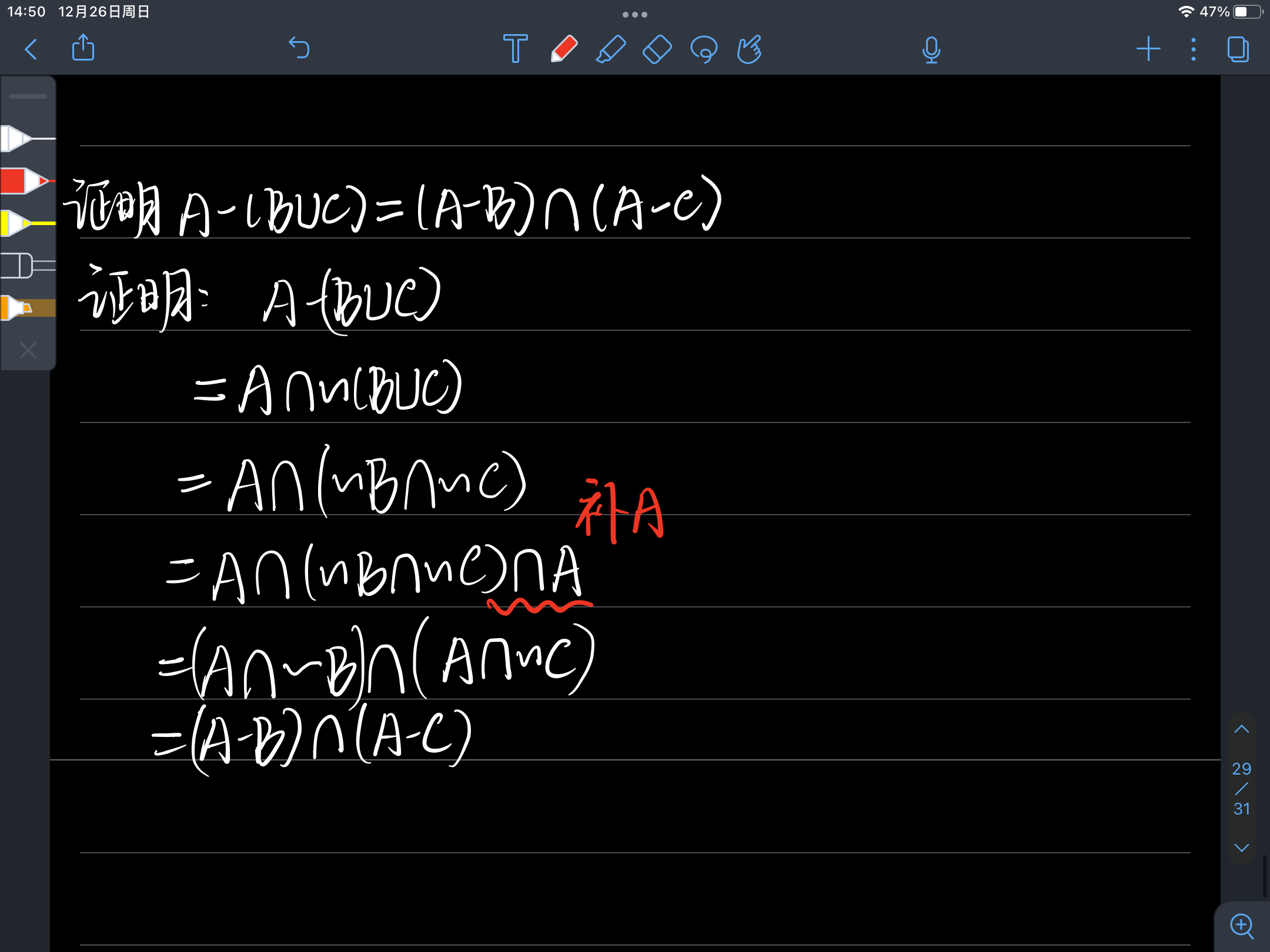
并运算
交运算
差运算
对称差：

A的绝对补集：在全集E中将A中的所有元素去除

例题：集合间的运算

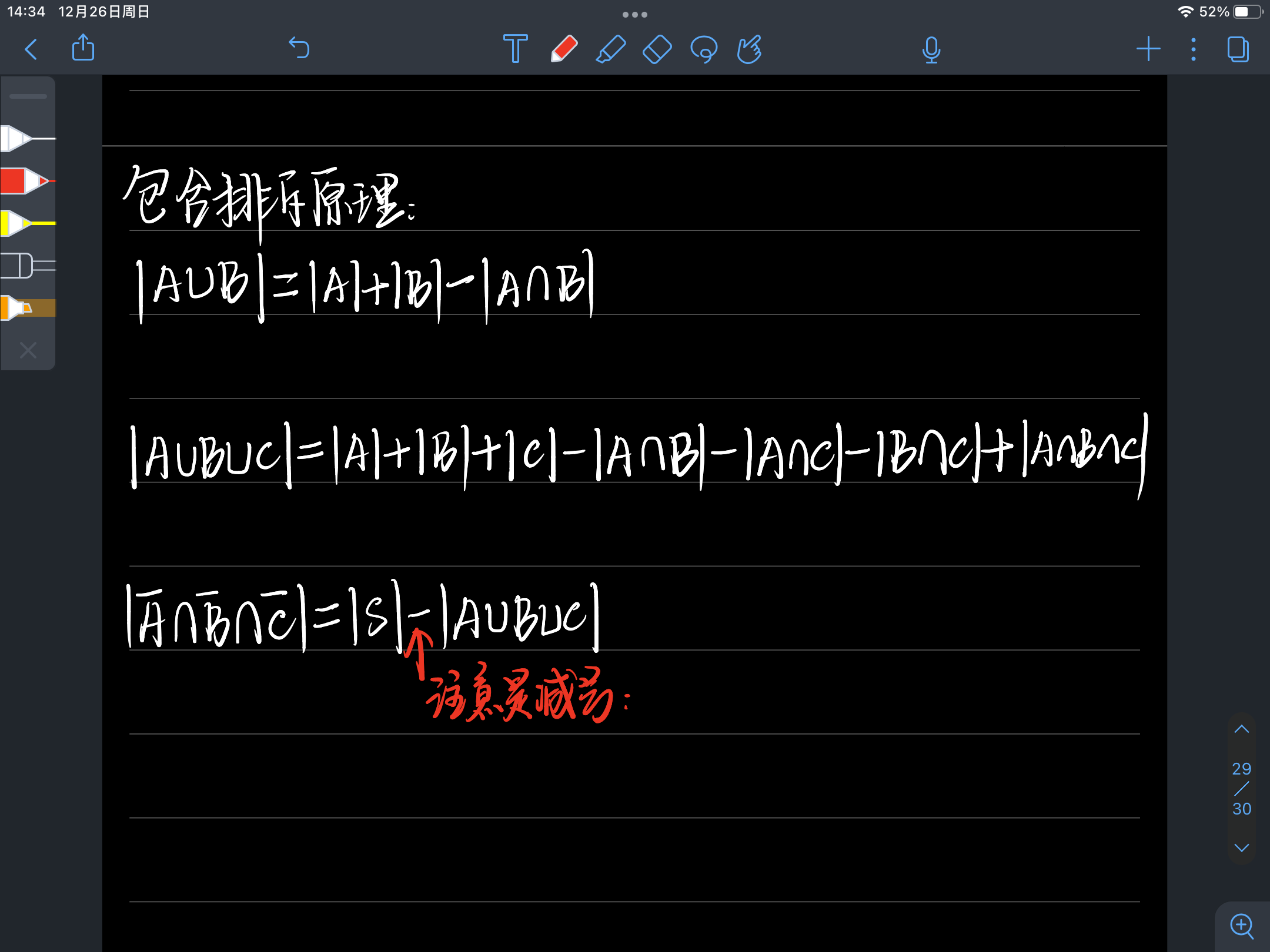
3、包含排斥原理

例题：使用包含排斥原理来统计集合的个数

4、集合恒等式