把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。输入一个递增排序的数组的一个旋转，输出旋转数组的最小元素。例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转，该数组的最小值为1。

    • 旋转之后的数组实际上可以划分为两个排序的子数组，而且前面的子数组的元素都大于或者等于后面子数组的元素
    • 最小的元素刚好是这两个子数组的分界线。
    • 排序的数组中我们可以用二分查找法实现O（logn）的查找

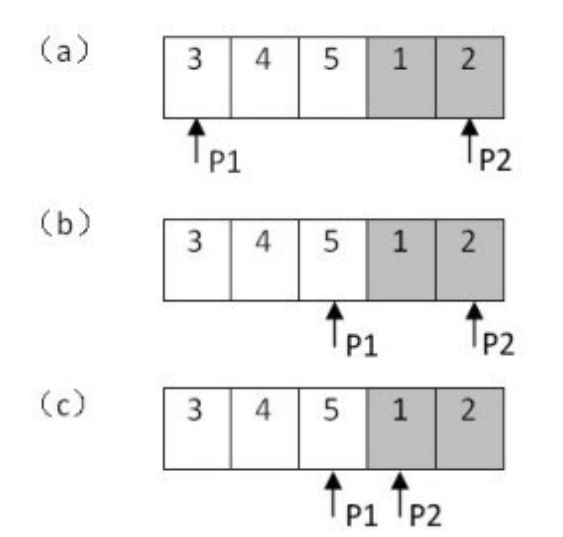
    image.png

    • 第一个指针已经指向了第一个递增子数组的末尾，而第二个指针指向第二个递增子数组的开头。第二个子数组的第一个数字就是最小的数字，因此第二个指针指向的数字就是我们查找的结果
    1. int Min(int *numbers, int length)
    2. {
    3.     if(numbers == NULL || length <= 0)
    4.         throw new std::exception("invalid parameters");
    6.     int index1 = 0;
    7.     int index2 = length - 1;
    8.     int indexMid = index1;
    9.     while(numbers[index1] >= numbers[index2])
    10.     {
    11.         if(index2 - index1 == 1)
    12.         {
    13.             indexMid = index2;
    14.             break;
    15.         }
    17.         indexMid = (index1 + index2) / 2;
    18.         if(numbers[indexMid] >= numbers[index1])
    19.             index1 = indexMid;
    20.         else if(numbers[indexMid <= numbers[index2]])
    21.             index2 = indexMid;
    22.     }
    24.     return numbers[indexMid];
    25. }
    • 仔细分析下标为index1和index2的两个数相同的情况。在前面的代码中，当这两个数相同，并且它们中间的数字（即indexMid指向的数字）也相同时，我们把indexMid赋值给了 index1，也就是认为此时最小的数字位于中间数字的后面。是不是一定这样？

    当两个指针指向的数字及它们中间的数字三者相同的时候，我们无法判断中间的数字是位于前面的子数组中还是后面的子数组中，也就无法移动两个指针来缩小查找的范围。此时，我们不得不采用顺序查找的方法。

    1. int Min(int *numbers, int length)
    2. {
    3.     if(numbers == NULL || length <= 0)
    4.         throw new std::exception("Invalid parameters");
    6.     int index1 = 0;
    7.     int index2 = length -1;
    8.     int indexMid = index1;
    9.     while(numbers[index1] >= numbers[index2])
    10.     {
    11.         if(index2 - index1 == 1)
    12.         {
    13.             indexMid = index2;
    14.             break;
    15.         }
    16.         indexMid = (index1 + index2) / 2;
    17.         // 如果下标为index1、index2和indexMid指向的三个数字相等，则只能顺序查找、
    18.         if(numbers[index1] == numbers[index2] && numbers[indexMid] == numbers[index1])
    19.             return MinInorder(numbers, index1, index2);
    21.          if(numbers[indexMid] >= numbers[index1])
    22.             index1 = indexMid;
    23.          else if(numbers[indexMid <= numbers[index2]])
    24.             index2 = indexMid;
    25.     }
    26.     return numbers[indexMid];
    27. }
    29. /* 顺序查找  */
    30. int MinInOrder(int *numbers, int index1, int index2)
    31. {
    32.     int result = numbers[index1];
    33.     for(int i=index1+1; i<=index2; ++i)
    34.     {
    35.         if(result > numbers[i])
    36.             result = numbers[i];
    37.     }
    39.     return result;
    40. }