知识点

前缀和

• 一维
  • S[i] = a[1] + a[2] + … a[i]
  • a[l] + … + a[r] = S[r] - S[l - 1]

• 二维

  • S[i, j] = 第i行j列格子左上部分所有元素的和
  • 以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为：S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]

    差分

• 一维

  • 差分数列B定义为：B[1] = A[1]，B[i] = A[i] - A[i - 1], 2 <= i <= n
  • 给区间[l, r]中的每个数加上c：B[l] += c, B[r + 1] -= c
• 二维

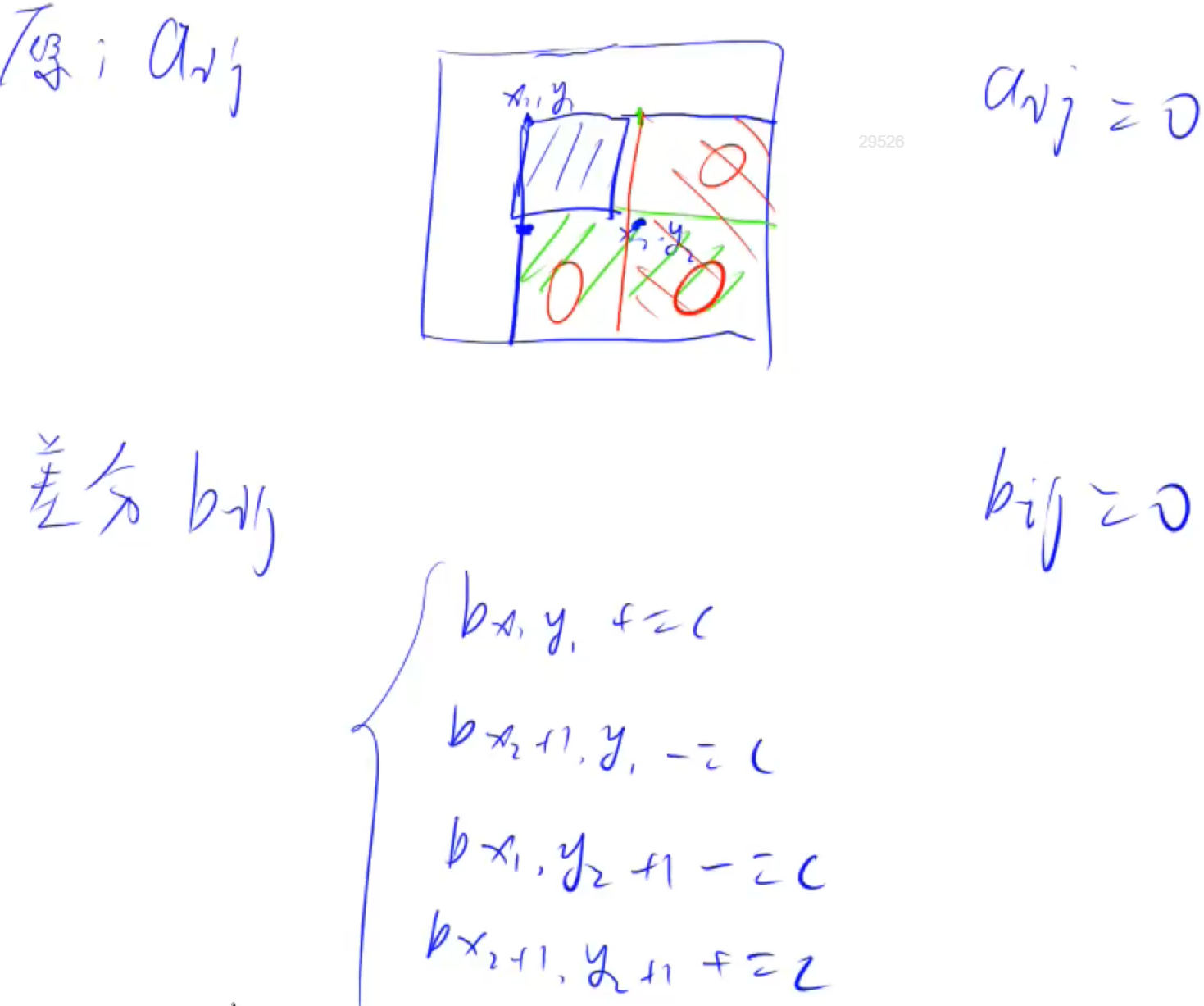
• 给以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵中的所有元素加上c：S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c

  例题

  前缀和

  激光炸弹

  直接从左上到右下递推出整个前缀和，然后枚举出最大值
  需要注意，目标在地图上的位置可能重合，因此是累加而不是直接赋值
  炸弹的范围可能非常大，因此需要缩小枚举的空间到地图最大范围（右下角） ```cpp

  include

using namespace std;

const int N = 5010;

int s[N][N];

int main() { int n, r; cin >> n >> r;

r = min(r, 5001);
int a = 0, b = 0;
while (n--) {
    int x, y, w;
    scanf("%d%d%d", &x, &y, &w);
    x++, y++;
    a = max(a, x), b = max(b, y);
    s[x][y] += w;
}
a = max(a, r), b = max(b, r);
for (int i = 1; i <= a; i++)
    for (int j = 1; j <= b; j++)
        s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
int res = 0;
for (int i = r; i <= a; i++)
    for (int j = r; j <= b; j++)
        res = max(res, s[i][j] - s[i - r][j] - s[i][j - r] + s[i - r][j - r]);
cout << res;
return 0;

}

<a name="Fl42b"></a>
## 差分
<a name="ESKRQ"></a>
### [增减序列](https://www.acwing.com/problem/content/102/)
记差分序列中正数总和为p，负数的绝对值总和为q<br />差分是区间边界上一个加一个减，因此首先要尽可能选择差分序列中一正一负的两个点，共操作min(p, q)次<br />只剩下正的或者是负的的时候，记这个位置为a，可以有两种选择：[0, a - 1]和[a, n]，共操作|p - q|次，对应|p - q| + 1种不同结果
```cpp
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
int a[N];
int main() {
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
    }
    LL pos = 0, neg = 0;
    for (int i = 2; i <= n; i++) {
        int d = a[i] - a[i - 1];
        if (d > 0) {
            pos += d;
        } else if (d < 0) {
            neg += -d;
        }
    }
    cout << max(pos, neg) << endl << abs(pos - neg) + 1;
    return 0;
}

最高的牛

每头牛身高尽可能高，那就先假设每头牛的身高和最高的那头牛一样
然后对于每一对关系，相当于两个端点的区间内牛的身高至少要减1，可以用差分来做
最后求一遍前缀和就得到了每头牛的身高
注意可能存在重复的关系
在unordered_set里面不能直接使用pair

#include <iostream>
#include <set>
using namespace std;
typedef pair<int, int> PII;
const int N = 1e4 + 10;
int h[N];
set<PII> exist;
int main() {
    int n, p, H, m;
    cin >> n >> p >> H >> m;
    h[0] = H;
    for (int i = 1; i <= m; i++) {
        int a, b;
        scanf("%d%d", &a, &b);
        if (a > b) swap(a, b);
        if (!exist.count({a, b})) {
            exist.insert({a, b});
            h[a + 1]--;
            h[b]++;
        }
    }
    for (int i = 1; i <= n; i++) {
        h[i] += h[i - 1];
        printf("%d\n", h[i]);
    }
    return 0;
}