理论

基于统计特征的熵函数是衡量图像信息丰富程度的一个重要指标，有信息论可知，一幅图像熵函数 - 图1的信息量是由该图像的信息熵熵函数 - 图2来度量：
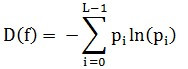
熵函数 - 图3
其中：熵函数 - 图4是图像中灰度值为熵函数 - 图5的像素出现的概率，熵函数 - 图6为灰度级总数（通常取值256）。根据Shannon信息论，熵最大时信息量最多。将此原理应用到对焦过程，熵函数 - 图7越大则图像越清晰。熵函数灵敏度不高，依据图像内容不同容易出现与真实情况相反的结果。
https://blog.csdn.net/Real_Myth/article/details/50827940

代码

  1. def entropy(img):
  2.     '''
  3.     :param img:narray 二维灰度图像
  4.     :return: float 图像约清晰越大
  5.     '''
  6.     out = 0
  7.     count = np.shape(img)[0]*np.shape(img)[1]
  8.     p = np.bincount(np.array(img).flatten())
  9.     for i in range(0, len(p)):
  10.         if p[i]!=0:
  11.             out-=p[i]*math.log(p[i]/count)/count
  12.     return out

https://blog.csdn.net/Greepex/article/details/90183018

9. 熵函数

基于统计特征的熵函数是衡量图像信息丰富程度的一个重要指标，有信息论可知，一幅图像 f 的信息量是由该图像的信息熵 D(f) 来度量:
熵函数 - 图8
其中：Pi 是图像中灰度值为i的像素出现的概率，L为灰度级总数（通常取值256）。根据Shannon信息论，熵最大时信息量最多。将此原理应用到对焦过程，D(f)越大则图像越清晰。熵函数灵敏度不高，依据图像内容不同容易出现与真实情况相反的结果。

代码：

  1. def Entropy(img):
  2.         x, y = img.shape
  3.         temp = np.zeros((1,256))
  5.         # 对图像的灰度值在[0,255]上做统计
  6.         for i in range(x):
  7.             for j in range(y):
  8.                 if img[i,j] == 0:
  9.                     k = 1
  10.                 else:
  11.                     k = img[i,j]
  12.                 temp[0,k] = temp[0,k] + 1
  13.         temp = temp / (x * y)
  15.         # 由熵的定义做计算
  16.         D = 0
  17.         for i in range(1,256):
  18.             if temp[0,i] != 0:
  19.                 D = D - temp[0,i] * math.log(temp[0,i],2)
  21.         return D

https://gist.github.com/JuneoXIE/d595028586eec752f4352444fc062c44