线段树

线段树

什么是线段树

线段树（英语：Segment tree）是一种二叉树形数据结构，1977年由Jon Louis Bentley发明[1]，用以存储区间或线段，并且允许快速查询结构内包含某一点的所有区间。

一个包含n个区间的线段树，空间复杂度为O(n)，查询的时间复杂度则为O(logn+k)},其中k是匹配条件的区间数量。

此数据结构亦可推广到高维度。

摘自《维基百科》

为什么要使用线段树

线段树的时间复杂度分析：

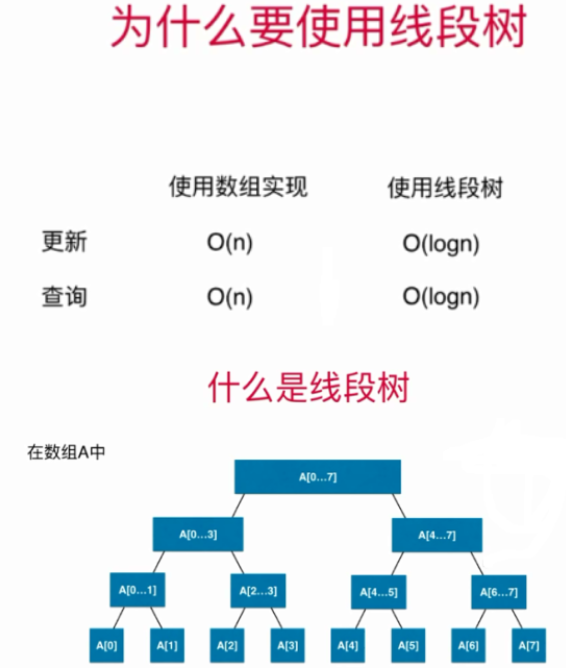
线段树基础表示

如果区间有n个元素，用数组表示线段树，需要多少结点？

0层：1

1层：2

2层：4

3层：8

…

h-1层：2^(h-1)

对于满二叉树：

h层，一共有2h）

最后一层(h-1)，有2^(h-1)个结点

最后一层的结点数大致等于前面所有层的结点数之和

**由此，可得出结论，我们线段树不考虑添加元素，即区间固定，使用4n的静态空间即可。

public class SegmentTree<E> {
    private E[] tree;
    private E[] data;
    public SegmentTree(E[] arr){
        data=(E[])new Object[arr.length];
        for(int i=0;i<arr.length;i++){
            data[i]=arr[i];
        }
        tree=(E[])new Object[4*arr.length];
    }
    public int getSize(){
        return data.length;
    }
    public E get(int index){
        if(index<0 || index>=data.length){
            throw new IllegalArgumentException("Index is illegal");
        }
        return data[index];
    }
    //返回完全二叉树的数组表示，一个索引所表示的元素的左孩子结点的索引
    public int leftChild(int index){
        return 2*index+1;
    }
    //返回完全二叉树的数组表示，一个索引所表示的元素的右孩子结点的索引
    public int rightChild(int index){
        return 2*index+2;
    }
}

创建线段树

public class SegmentTree<E> {
    private E[] tree; //存储线段树中数据
    private E[] data;
    private Merger<E> merger;
    public SegmentTree(E[] arr, Merger<E> merger){
        this.merger=merger;
        data=(E[])new Object[arr.length];
        for(int i=0;i<arr.length;i++){
            data[i]=arr[i];
        }
        tree=(E[])new Object[4*arr.length];
        buildSegmentTree(0,0,data.length-1);
    }
    //在treeIndex根节点的位置创建区间在[l,r]的线段树
    private void buildSegmentTree(int treeIndex,int l,int r){
        if(l==r){
            tree[treeIndex]=data[l];
            return;
        }
        int leftTreeIndex=leftChild(treeIndex);
        int rightTreeIndex=rightChild(treeIndex);
        int mid=l+(r-l)/2;
        //创建左子树的线段树
        buildSegmentTree(leftTreeIndex,l,mid);
        //创建右子树的线段树
        buildSegmentTree(rightTreeIndex,mid+1,r);
        //当左右子树创建完成之后，综合左右子树的结果，
        //如何去综合是由业务逻辑去决定的。
        tree[treeIndex]=merger.meger(tree[leftTreeIndex],tree[rightTreeIndex]);
    }
    public int getSize(){
        return data.length;
    }
    public E  get(int index){
        if(index<0 || index>=data.length){
            throw new IllegalArgumentException("Index is illegal");
        }
        return data[index];
    }
    //在完全二叉树的数组表示中，获取左孩子节点的索引
    private int leftChild(int index){
        return 2*index+1;
    }
    //在完全二叉树的数组表示中，获取右孩子节点的索引
    private int rightChild(int index){
        return 2*index+2;
    }
    @Override
    public String toString() {
        StringBuilder res=new StringBuilder();
        res.append("[");
        for(int i=0;i<tree.length;i++){
            if(tree[i]!=null){
                res.append(tree[i]);
            }else{
                res.append("null");
            }
            if(i!=tree.length-1){
                res.append(", ");
            }
        }
        res.append("]");
        return res.toString();
    }
}

线段树的合并器接口
融合器，根据业务逻辑来融合左右子树的内容

public interface Merger<E> {
    E meger(E a,E b);
}

线段树的查询

//查询区间[queryL,queryR]的值
public E query(int queryL, int queryR){
    if(queryL<0 || queryL>=data.length
            || queryR<0 || queryR>=data.length || queryL>queryR){
        throw new IllegalArgumentException("Index is illegal");
    }
    return query(0,0,data.length-1,queryL,queryR);
}
//以treeIndex为根的线段树[l...r]的范围搜索[queryL,queryR]区间
private E query(int treeIndex,int l,int r,int queryL,int queryR){
    //搜索到目标区间
    if(l==queryL && r==queryR){
        return tree[treeIndex];
    }
    int mid=l+(r-l)/2;
    int leftTreeIndex=leftChild(treeIndex);
    int rightTreeIndex=rightChild(treeIndex);
    if(queryL>=mid+1){
        //仅在右部分
        return query(rightTreeIndex,mid+1,r,queryL,queryR);
    }else if(queryR<=mid){
        //仅在左部分
        return query(leftTreeIndex,l,mid,queryL,queryR);
    }
    //剩下的情况是：有部分落在左区间，另一部分落在右区间
    //在左子树中寻找
    E leftResult=query(leftTreeIndex,l,mid,queryL,mid);
    //在右子树中寻找
    E rightResult=query(rightTreeIndex,mid+1,r,mid+1,queryR);
    return merger.merge(leftResult,rightResult);
}

线段树的更新

//更新index位置的值
public void set(int index,E e){
    if(index<0 || index>data.length){
        throw new IllegalArgumentException("Index is illegal");
    }
    set(0,0,data.length-1,index,e);
}
//更新以treeIndex为根的线段树[l...r]的值为e
private void set(int treeIndex,int l,int r,int index,E e){
    //搜索到目标，直接更新
    if(l==r){
        tree[treeIndex]=e;
        return;
    }
    int mid=l+(r-l)/2;
    int leftTreeIndex=leftChild(treeIndex);
    int rightTreeIndex=rightChild(treeIndex);
    if(index>=mid+1){
        //继续到右子树更新
        set(rightTreeIndex,mid+1,r,index,e);
    }else if(index<=mid){
        //继续到左子树更新
        set(leftTreeIndex,l,mid,index,e);
    }
    //更新祖辈节点
    tree[treeIndex]=merger.merge(tree[leftTreeIndex],tree[rightTreeIndex]);
}

LeetCode中有关线段树的问题

LeetCode 303题区域和检索 - 数组不可变

public class NumArray {
    private SegmentTree<Integer> segmentTree;
    public NumArray(int[] nums) {
        if(nums.length>0){
            Integer[] data=new Integer[nums.length];
            for(int i=0;i<nums.length;i++){
                data[i]=nums[i];
            }
            segmentTree=new SegmentTree<Integer>(data,(a,b)-> a+b);
        }
    }
    public int sumRange(int i, int j) {
        if(segmentTree==null){
            throw new IllegalArgumentException("Segment Tree is null");
        }
        return segmentTree.query(i,j);
    }
}

LeetCode 307题区域和检索 - 数组可修改

Huang Java 开发学习

线段树Segment tree

线段树