回归预测燃油效率
TF2.0 TensorFlow 2 / 2.0 文档:Regression 回归
主要内容:使用回归预测烟油效率。
回归通常用来预测连续值,比如价格和概率。分类问题不一样,类别是固定的,目的是判断属于哪一类。比如给你一堆猫和狗的图片,判断一张图片是猫还是狗就是一个典型的分类问题。
接下来使用的是经典的 Auto MPG 数据集,这个数据集包括气缸(cylinders),排量(displayment),马力(horsepower) 和重量(weight)等属性。我们需要利用这些属性搭建模型,预测汽车的燃油效率(fuel efficiency)。
模型搭建使用tf.keras API。
import pathlibimport matplotlib.pyplot as pltimport pandas as pdimport seaborn as snsimport tensorflow as tffrom tensorflow import kerasfrom tensorflow.keras import layers
Auto MPG 数据集
获取数据
# 下载数据集到本地url = "http://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data"dataset_path = keras.utils.get_file("auto-mpg.data", url)# 使用Pandas读取数据column_names = ['MPG','气缸','排量','马力','重量','加速度', '年份', '产地']raw_dataset = pd.read_csv(dataset_path, names=column_names,na_values = "?", comment='\t',sep=" ", skipinitialspace=True)dataset = raw_dataset.copy()# 查看前3条数据dataset.head(3)
| MPG | 气缸 | 排量 | 马力 | 重量 | 加速度 | 年份 | 产地 | |
|---|---|---|---|---|---|---|---|---|
| 0 | 18.0 | 8 | 307.0 | 130.0 | 3504.0 | 12.0 | 70 | 1 |
| 1 | 15.0 | 8 | 350.0 | 165.0 | 3693.0 | 11.5 | 70 | 1 |
| 2 | 18.0 | 8 | 318.0 | 150.0 | 3436.0 | 11.0 | 70 | 1 |
清洗数据
检查是否有 NA 值。
dataset.isna().sum()
MPG 0气缸 0排量 0马力 6重量 0加速度 0年份 0产地 0dtype: int64
直接去除含有NA值的行(马力)
dataset = dataset.dropna()
在获取的数据集中,Origin(产地)不是数值类型,需转为独热编码。
origin = dataset.pop('产地')dataset['美国'] = (origin == 1)*1.0dataset['欧洲'] = (origin == 2)*1.0dataset['日本'] = (origin == 3)*1.0# 看一看转换后的结果dataset.head(3)
| MPG | 气缸 | 排量 | 马力 | 重量 | 加速度 | 年份 | 美国 | 欧洲 | 日本 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 18.0 | 8 | 307.0 | 130.0 | 3504.0 | 12.0 | 70 | 1.0 | 0.0 | 0.0 |
| 1 | 15.0 | 8 | 350.0 | 165.0 | 3693.0 | 11.5 | 70 | 1.0 | 0.0 | 0.0 |
| 2 | 18.0 | 8 | 318.0 | 150.0 | 3436.0 | 11.0 | 70 | 1.0 | 0.0 | 0.0 |
划分训练集与测试集
# 训练集 80%, 测试集 20%train_dataset = dataset.sample(frac=0.8, random_state=0)test_dataset = dataset.drop(train_dataset.index)
检查数据
快速看一看训练集中属性两两之间的关系吧。
# 解决中文乱码问题plt.rcParams['font.sans-serif']=['SimHei']plt.rcParams['axes.unicode_minus']=Falsesns.pairplot(train_dataset[["MPG", "气缸", "排量", "重量"]], diag_kind="kde")
matplotlib 中文乱码看这里:matplotlib图例中文乱码?
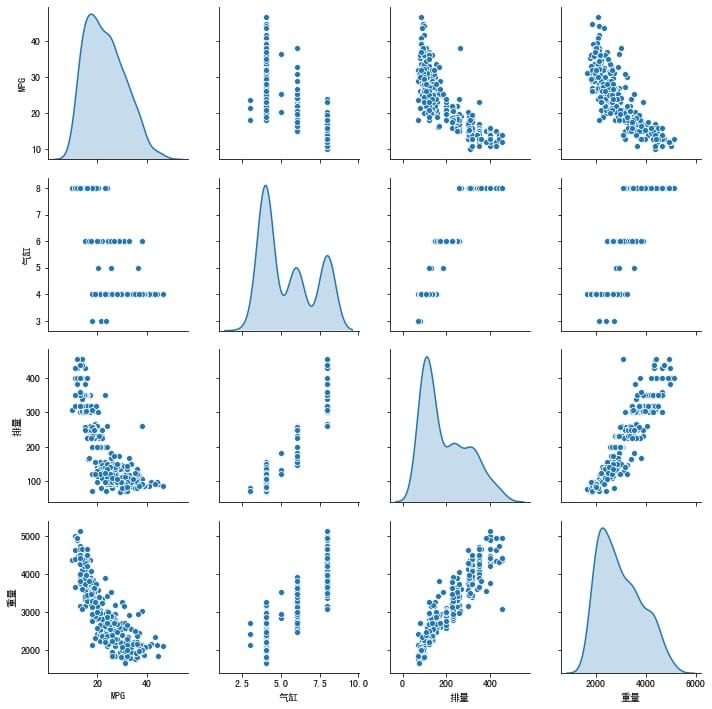
你还可以使用train_dataset.describle()快速浏览每一属性的平均值、标准差、最小值、最大值等信息,能够帮助你快速地识别出不合理的数据。
train_stats = train_dataset.describe()train_stats.pop("MPG")train_stats = train_stats.transpose()train_stats
| count | mean | std | min | 25% | 50% | 75% | max | |
|---|---|---|---|---|---|---|---|---|
| 气缸 | 314.0 | 5.477707 | 1.699788 | 3.0 | 4.00 | 4.0 | 8.00 | 8.0 |
| 排量 | 314.0 | 195.318471 | 104.331589 | 68.0 | 105.50 | 151.0 | 265.75 | 455.0 |
| … | … | … | … | … | … | …. | … | … |
分离 label
# 分离 labeltrain_labels = train_dataset.pop('MPG')test_labels = test_dataset.pop('MPG')
归一化数据
通常训练前需要归一化数据,不同属性使用的计量单位不一样,值的范围不一样,训练就会很困难。比如其中一个属性的范围是[0.1, 0.5],而另一个属性的范围是[1000, 5000],那数值大的属性就容易对训练产生干扰,很可能导致训练不能收敛,或者是数值小的属性在模型中几乎没有发挥作用。归一化将不同范围的数据映射到[0,1]的空间内,可以有效地避免这个问题。
def norm(x):return (x - train_stats['mean']) / train_stats['std']normed_train_data = norm(train_dataset)normed_test_data = norm(test_dataset)
模型
搭建模型
我们的模型包含2个全连接的隐藏层构成,输出层返回一个连续值。
def build_model():input_dim = len(train_dataset.keys())model = keras.Sequential([layers.Dense(64, activation='relu', input_shape=[input_dim,]),layers.Dense(64, activation='relu'),layers.Dense(1)])model.compile(loss='mse', metrics=['mae', 'mse'],optimizer=tf.keras.optimizers.RMSprop(0.001))return modelmodel = build_model()# 打印模型的描述信息,每一层的大小、参数个数等model.summary()
Model: "sequential_1"_________________________________________________________________Layer (type) Output Shape Param #=================================================================dense_4 (Dense) (None, 64) 640_________________________________________________________________dense_5 (Dense) (None, 32) 2080_________________________________________________________________dense_6 (Dense) (None, 1) 33=================================================================Total params: 2,753Trainable params: 2,753Non-trainable params: 0_________________________________________________________________
训练模型
在之前的案例,比如结构化数据分类,我们调用model.fit会打印出训练的进度。我们可以禁用默认的行为,并自定义训练进度条。
import sysEPOCHS = 1000class ProgressBar(keras.callbacks.Callback):def on_epoch_end(self, epoch, logs):# 显示进度条self.draw_progress_bar(epoch + 1, EPOCHS)def draw_progress_bar(self, cur, total, bar_len=50):cur_len = int(cur / total * bar_len)sys.stdout.write("\r")sys.stdout.write("[{:<{}}] {}/{}".format("=" * cur_len, bar_len, cur, total))sys.stdout.flush()history = model.fit(normed_train_data, train_labels,epochs=EPOCHS, validation_split = 0.2, verbose=0,callbacks=[ProgressBar()])
[==================================================] 1000/1000
训练过程都存储在了history对象中,我们可以借助 matplotlib 将训练过程可视化。
hist = pd.DataFrame(history.history)hist['epoch'] = history.epochhist.tail(3)
| loss | mae | mse | val_loss | val_mae | val_mse | epoch | |
|---|---|---|---|---|---|---|---|
| 997 | 3.132053 | 1.142280 | 3.132053 | 9.711935 | 2.361466 | 9.711935 | 997 |
| 998 | 3.021109 | 1.093424 | 3.021109 | 9.488593 | 2.298264 | 9.488593 | 998 |
| 999 | 3.028849 | 1.132241 | 3.028849 | 9.453931 | 2.275017 | 9.453931 | 999 |
def plot_history(history):hist = pd.DataFrame(history.history)hist['epoch'] = history.epochplt.figure()plt.xlabel('epoch')plt.ylabel('metric - MSE')plt.plot(hist['epoch'], hist['mse'], label='训练集')plt.plot(hist['epoch'], hist['val_mse'], label = '验证集')plt.ylim([0, 20])plt.legend()plt.figure()plt.xlabel('epoch')plt.ylabel('metric - MAE')plt.plot(hist['epoch'], hist['mae'], label='训练集')plt.plot(hist['epoch'], hist['val_mae'], label = '验证集')plt.ylim([0, 5])plt.legend()plot_history(history)
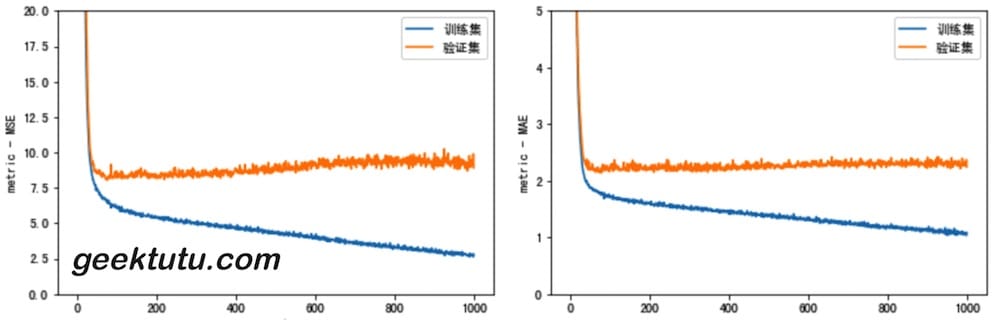
从图中,我们可以看到,从100 epoch开始,训练集的loss仍旧继续降低,但验证集的loss却在升高,说明过拟合了,训练应该早一点结束。接下来,我们使用 keras.callbacks.EarlyStopping,每一波(epoch)训练结束时,测试训练情况,如果训练不再有效果(验证集的loss,即val_loss 不再下降),则自动地停止训练。
model = build_model()early_stop = keras.callbacks.EarlyStopping(monitor='val_loss', patience=10)history = model.fit(normed_train_data, train_labels, epochs=EPOCHS,validation_split = 0.2, verbose=0,callbacks=[early_stop, ProgressBar()])plot_history(history)
[=== ] 70/1000
在第 70 epoch 时,停止了训练。
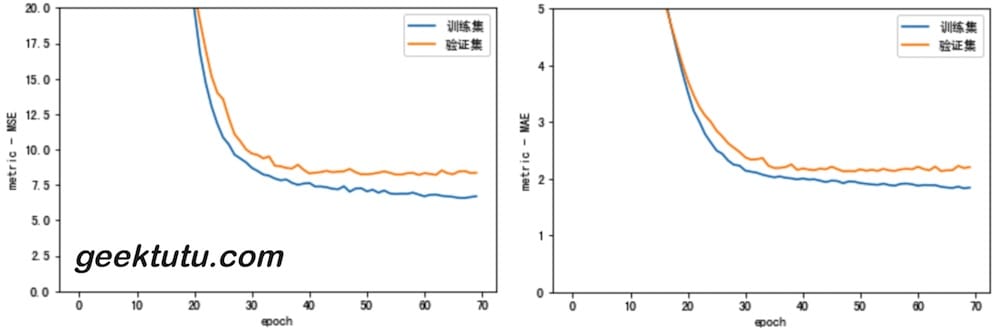
接下来使用测试集来评估训练效果。
loss, mae, mse = model.evaluate(normed_test_data, test_labels, verbose=0)print("测试集平均绝对误差(MAE): {:5.2f} MPG".format(mae))# 测试集平均绝对误差(MAE): 1.90 MPG
从图中我们也可以看出,1.9比验证集还略低一点。
预测
最后,我们使用测试集中的数据来预测 MPG 值。
test_pred = model.predict(normed_test_data).flatten()plt.scatter(test_labels, test_pred)plt.xlabel('真实值')plt.ylabel('预测值')plt.axis('equal')plt.axis('square')plt.xlim([0,plt.xlim()[1]])plt.ylim([0,plt.ylim()[1]])plt.plot([-100, 100], [-100, 100])
看起来,模型训练得还不错。
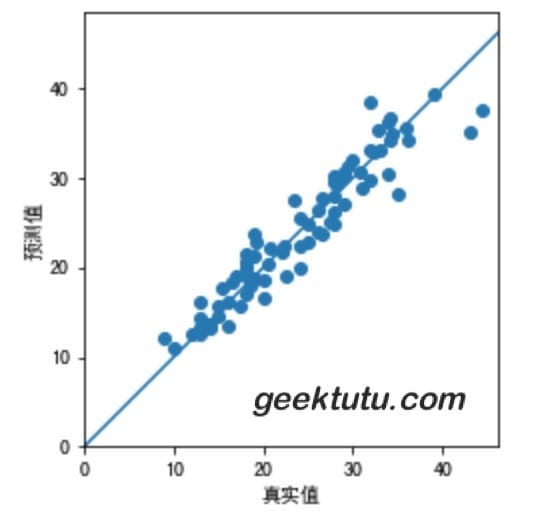
结论
- 均方误差(Mean Squared Error, MSE) 常作为回归问题的损失函数(loss function),与分类问题不太一样。
- 同样,评价指标(evaluation metrics)也不一样,分类问题常用准确率(accuracy),回归问题常用平均绝对误差 (Mean Absolute Error, MAE)
- 每一列数据都有不同的范围,每一列,即每一个feature的数据需要分别缩放到相同的范围。常用归一化的方式,缩放到[0, 1]。
- 如果训练数据过少,最好搭建一个隐藏层少的小的神经网络,避免过拟合。
- 早停法(Early Stoping)也是防止过拟合的一种方式。
返回文档首页
完整代码:Github - auto_mpg_regression.ipynb 参考文档:Regression: Predict fuel efficiency

