Other - 基于遗传算法实现自动组卷 - 《.Net 学习历程》

一、遗传算法介绍
- 1.1 遗传算法概要
- 1.2 遗传算法的基本操作
二、自动组卷的实现
三、实例讲解遗传算法——基于遗传算法的自动组卷系统">三、实例讲解遗传算法——基于遗传算法的自动组卷系统
3、开始遗传算法组卷之旅">3、开始遗传算法组卷之旅

一、遗传算法介绍

1.1 遗传算法概要

遗传算法是模拟达尔文的遗传选择和自然淘汰的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法，它是用来解决多约束条件下的最优问题。

遗传算法是从代表问题可能潜在的解集的一个种群开始的，而一个种群则由经过基因编码的一定数目的个体组成。每个个体实际上是染色体带有特征的实体。染色体作为遗传物质的主要载体，即多个基因的集合，它决定了个体的形状的外部表现。因此，在一开始需要实现从表现型到基因型的映射即编码工作。由于仿照基因编码的工作很复杂，往往进行简化，如二进制编码，初始种群产生之后，按照适者生存和优胜劣汰的原理，逐代演化产生出越来越好的近似解，在每一代，根据问题域中个体的适应度大小挑选个体，并借助于自然遗传学的遗传算子进行组合交叉和变异，产生出代表新的解集的种群。这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境，末代种群中的最优个体经过解码，可以作为问题近似最优解。

 遗传算法提供了一种求解复杂系统优化问题的通用框架。它不依赖于问题的具体领域，对问题的种类有很强的鲁棒性，所以广泛应用于很多学科。遗传算法的主要应用领域有：函数优化、组合优化、生产调度问题、自动控制、机器人自动控制、图像处理和模式识别、人工生命、遗传程序设计、机器学习。

1.2 遗传算法的基本操作

遗传算法有三个基本操作：选择、交叉、变异。这些操作又有不同的方法来实现。

（1）选择。选择是用来确定重组或交叉的个体，以及被选个体将产生多少子个体。首选计算适应度：按比例的适应度计算；基于排序的适应度计算。适应度计算之后是实际的选择，按照适应度进行父代个体的选择。可以挑选以下算法：轮盘赌选择、随机遍历抽样、局部选择、截断选择、锦标赛选择。

（2）交叉。基因重组是结合来自父代交配种群中的信息产生新的个体。依据个体编码表示方法的不同，可以有以下的算法：实值重组；离散重组；中间重组；线性重组；扩展线性重组。二进制交叉、单点交叉、多点交叉、均匀交叉、洗牌交叉、缩小代理交叉。

（3）变异。交叉之后子代经历的变异，实际上是子代基因按小概率扰动产生的变化。依据个体编码表示方法的不同，可以有以下的算法：实值变异、二进制变异。

二、自动组卷的实现

自动组卷是根据用户给定的约束条件（总时间、难度系数、考试时间、考试章节、题型比例等），搜索试题库中与特征参数相匹配的试题，从而抽取最优的试题组合。由此可见，自动组卷问题是一个具有多重约束的组合优化问题。

传统的遗传算法存在搜索后期效率低和易形成末成熟收敛的情况。根据具体情况和需求分析要求，对遗传算法进了稍微改进，表现为采用实数编码、分段交叉、有条件生成初始种群。具体解决方案如下。

2.1 染色体编码及初始群体的设计

用遗传算法求解问题，首先要将问题的解空间映射成一组代码串，即染色体的编码问题。在传统的遗传算法中采用二进制编码。用二进制编码时，题库里的每一道题都要出现在这个二进制位串中，1表示该题选中，0表示该题未被选中。这样的二进制位串较长，且在进行交叉和变异遗传算子操作时，各种题型的题目数量不好控制。采用实数编码方案，将一份试卷映射为一个染色体，组成该试卷的每道题的题号作为基因，基因的值直接用试题号表示，每种题型的题号放在一起，按题型分段，在随后的遗传算子操作时也按段进行，保证了每种题型的题目总数不变。比如，要组一份《C语言程序设计》试卷，其选择题5道，填空题5道，简答题3道，则染色体编码是：

(10、76、23、52、101 | 52、36、67、11、123 | 99、85、45)

选择题填空题简答题

试卷初始种群不是采用完全随机的方法产生，而是根据题型比例、总分、答题时间、知识点不重复、不考章节等要求随机产生，使得初始种群一开始就满足了题型、总分、答题时间和知识点等要求。这样加快遗传算法的收敛并减少迭代次数，由于不同的题型是从不同的题型表中取出，有可能在同一个基因串中会出现相同的试题编号，因它们属于不同题型，故这种情况是正常的，不影响组卷。采用分组实数编码，可以克服以往采用二进制编码搜索空间过大和编码长度过长的缺点，同时取消了个体的解码时间，提高了求解速度。

2.2 适应度函数的设计

 适应度函数是用来评判试卷群体中个体的优劣程度的指标，遗传算法利用适应度值这一信息来指导搜索方向，而不需要适应度函数连续或可导以及其它辅助信息。因为时间、章节等要求在初始化种群时已经考虑，这里只剩下难度系数要考虑的了。所以适应度函数由试卷难度系数公式转换而成。试卷难度系数公式：P=∑Di×Si/∑Si；其中i=1，2，....N，N是试卷所含的题目数，Ｄi，Ｓi分别是第i题的难度系数和分数。用户的期望难度系数EP与试卷难度系数P之差f越小越好，f=|EP-P|， 而适应度函数是值越大越好，因此将目标函数f转换成适应度函数F=e-0.03f，这种采用加权误差的适应度函数可以较好地反映求解组卷问题的特征，当试卷个体对各项组卷约束条件的误差越小时，它的适应度函数值就越大，则表示试卷个体越接近卷目标。

2.3 遗传算子的设计

（1）选择算子。选择算子的作用在于根据个体的优劣程度决定它在下一代是被淘汰还是被复制。通过选择，将使适应度高的个体有较大的生存机会。本系统采用轮盘赌方法，它是目前遗传算法中最常用也是最经典的选择方法。其具体实现为：规模为M的群体P={a1、a2、… am} ，其被选择概率为：

（2）交叉算子。由于在编码时采用的是分段实数编码，所以在进行交叉时采用分段单点交叉（按题型分段来进行交叉），整个染色体就表现为多点交叉。交叉的实现过程：将群体中的染色体任意进行两两配对，对每对染色体产生一个[0， 1 ]的随机数r，若r≤pc（据经验，pc值取0.6到0.8），则分段随机产生一个交叉点，然后分段进行互换以得到下一代。

交叉后生成的子代有可能因存在重复的题号而非法。出现这种情况要将出现的题号换成该段中没有出现过的题号，这样重新得到新子代。

（3）变异算子。在遗传算法中，变异概率一般较小。这里不分段进行变异，而是只对某段上的某个基因进行变异。对某个染色体，随机生成一个[0，1]范围内的实数r，若r≤pm（据经验，pm值取0.01到0.02），则对该染色体进行变异，否则不进行变异。变异的操作如下：在[1，n]范围内随机生成一个段号f，设该段的段长为L，则在[1，L]范围内随机生成一个变异位置P，以一定的原则从题库中选择一个变异基因，变异基因的选择原则为：与原基因题型相同的；满足答题时间相同；考试章节相同等要求。

2.4 算法的实现伪代码及实施流程图

确定参数：最大代数Max，群体规模N，交叉概率pc，变异概率pm，输入用户的组卷要求。算法实施流程如图1所示。

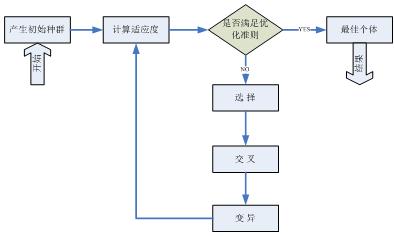
基于遗传算法实现自动组卷 - 图1
图1 算法实施流程图

2.5 界面设计与实现结果

系统试题库是C 语言试题。试题库中现有单选题、填空题、判断题、程序设计题、简答题等。群体规模设为20，算法执行的最大迭代次数设为200，交叉概率Pc设为0.7，变异概率Pm 设为0.015。用户定制试卷的界面如图2所示。

组卷的具体要求：试卷总分100，用时120min，试卷难度系数0.6，不考章节1.2。组卷结果表明，在进化到120代左右时即可生成一份满意的试卷且误差比较小，改进的遗传算法降低了组卷问题的求解难度，组卷效率高、成功率高；且算法对初值不敏感，具有较好的鲁棒性。在初始试卷生成之后，对有必考题要求，可以在试卷生成界面添加必考题。试卷生成界面如图3所示。

三、实例讲解遗传算法——基于遗传算法的自动组卷系统

先上两张运行后的效果图吧：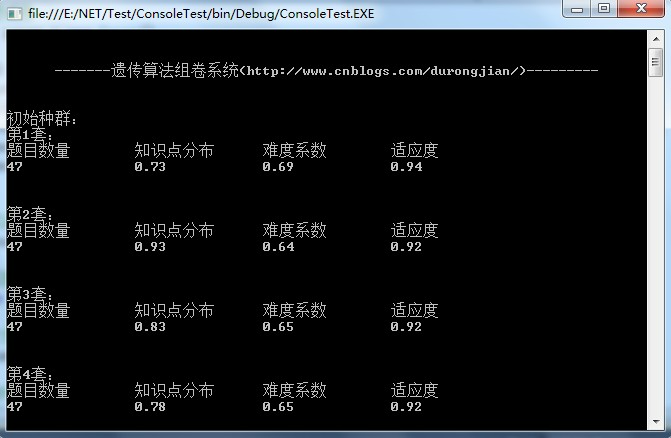

基于遗传算法实现自动组卷 - 图2

基于遗传算法的自动组卷系统运行效果图（1）

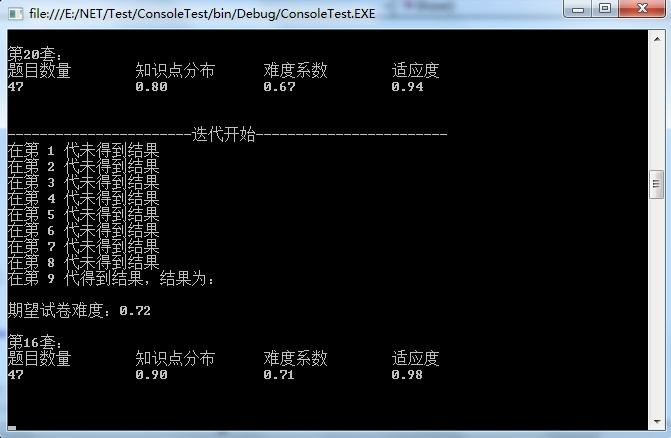
基于遗传算法实现自动组卷 - 图3

基于遗传算法的自动组卷系统运行效果图（2）

1、准备工作

1、问题实体

问题实体包含编号、类型（类型即题型，分为五种：单选，多选，判断，填空，问答，分别用1、2、3、4、5表示）、分数、难度系数、知识点。一道题至少有一个知识点，为简单易懂，知识点用List 表示（知识点编号集合）。代码如下：

public class Problem 
{undefined
public Problem()
{undefined
ID = 0;
Type = 0;
Score = 0;
Difficulty = 0.00;
Points = new List<int>();
}
public Problem(Problem p)
{undefined
this.ID = p.ID;
this.Type = p.Type;
this.Score = p.Score;
this.Difficulty = p.Difficulty;
this.Points = p.Points;
}
/// <summary>
/// 编号
/// </summary>
public int ID { get; set; }
/// <summary>
/// 题型（1、2、3、4、5对应单选，多选，判断，填空，问答）
/// </summary>
public int Type { get; set; }
/// <summary>
/// 分数
/// </summary>
public int Score { get; set; }
/// <summary>
/// 难度系数
/// </summary>
public double Difficulty { get; set; }
/// <summary>
/// 知识点
/// </summary>
public List<int> Points { get; set; }
}

2、题库

为了简单，这里没有用数据库，题目信息临时创建，保存在内存中。因为对不同层次的考生一道题目在不同试卷中的分数可能不一样，因此题目分数一般是老师出卷时定的，不保存在题库中。且单选，多选，判断题每题分数应该相同，填空题一般根据空数来定分数，而问答题一般根据题目难度来定的，因此这里的单选、多选、判断分数相同，填空空数取1-4间的随机数，填空题分数即为空数，问答题即为该题难度系数*10取整。这里各种题型均为1000题，具体应用时改为数据库即可。代码如下：

public class DB
{undefined
/// <summary>
/// 题库
/// </summary>
public List<Problem> ProblemDB;
public DB()
{undefined
ProblemDB = new List<Problem>();
Problem model;
Random rand = new Random();
List<int> Points;
for (int i = 1; i <= 5000; i++)
{undefined
model = new Problem();
model.ID = i;
//试题难度系数取0.3到1之间的随机值
model.Difficulty = rand.Next(30, 100) * 0.01;
//单选题1分
if (i < 1001)
{undefined
model.Type = 1;
model.Score = 1;
}
//单选题2分
if (i > 1000 && i < 2001)
{undefined
model.Type = 2;
model.Score = 2;
}
//判断题2分
if (i > 2000 && i < 3001)
{undefined
model.Type = 3;
model.Score = 2;
}
//填空题1—4分
if (i > 3000 && i < 4001)
{undefined
model.Type = 4;
model.Score = rand.Next(1, 5);
}
//问答题分数为难度系数*10
if (i > 4000 && i < 5001)
{undefined
model.Type = 5;
model.Score = model.Difficulty > 0.3 ? (int)(double.Parse(model.Difficulty.ToString("f1")) * 10) : 3;
}
Points = new List<int>();
//每题1到4个知识点
int count = rand.Next(1, 5);
for (int j = 0; j < count; j++)
{undefined
Points.Add(rand.Next(1, 100));
}
model.Points = Points;
ProblemDB.Add(model);
}
}
}

3、试卷实体

试卷一般包含试卷编号，试卷名称，考试时间，难度系数，知识点分布，总题数，总分数，各种题型所占比率等属性，这里为简单去掉了试卷名称跟考试时间。其中的知识点分布即老师出卷时选定本试卷要考查的知识点，这里用List（知识点编号集合）表示。代码如下：

public class Paper
{undefined
/// <summary>
/// 编号
/// </summary>
public int ID { get; set; }
/// <summary>
/// 总分
/// </summary>
public int TotalScore { get; set; }
/// <summary>
/// 难度系数
/// </summary>
public double Difficulty { get; set; }
/// <summary>
/// 知识点
/// </summary>
public List<int> Points { get; set; }
/// <summary>
/// 各种题型题数
/// </summary>
public int[] EachTypeCount { get; set; }
}

3、开始遗传算法组卷之旅

准备工作已经OK，下面就按上一篇介绍的流程进行操作啦！

1、产生初始种群

这里保证题数跟总分达到出卷要求即可，但为操作方便，这里再定义一个种群个体实体类Unit，包含编号、适应度、题数、总分、难度系数、知识点分布、包含的题目等信息（也可以修改一下试卷实体，用试卷实体表示）：

public class Unit
{undefined
public Unit()
{undefined
ID = 0;
AdaptationDegree = 0.00;
KPCoverage = 0.00;
ProblemList = new List<Problem>();
}
/// <summary>
/// 编号
/// </summary>
public int ID { get; set; }
/// <summary>
/// 适应度
/// </summary>
public double AdaptationDegree { get; set; }
/// <summary>
/// 难度系数（本试卷所有题目分数*难度系数/总分）
/// </summary>
public double Difficulty
{undefined
get
{undefined
double diff = 0.00;
ProblemList.ForEach(delegate(Problem p)
{undefined
diff += p.Difficulty * p.Score;
});
return diff / SumScore;
}
}
/// <summary>
/// 题目数量
/// </summary>
public int ProblemCount
{undefined
get
{undefined
return ProblemList.Count;
}
}
/// <summary>
/// 总分
/// </summary>
public int SumScore
{undefined
get
{undefined
int sum = 0;
ProblemList.ForEach(delegate(Problem p)
{undefined
sum += p.Score;
});
return sum;
}
}
/// <summary>
/// 知识点分布
/// </summary>
public double KPCoverage { get; set; }
/// <summary>
/// 题目
/// </summary>
public List<Problem> ProblemList { get; set; }
}

下面即来产生初始种群，按个体数量，期望试卷知识点分布，各类型题目数等限制产生初始种群：

/// <summary>
/// 初始种群
/// </summary>
/// <param name="count">个体数量</param>
/// <param name="paper">期望试卷</param>
/// <param name="problemList">题库</param>
/// <returns>初始种群</returns>
public List<Unit> CSZQ(int count, Paper paper, List<Problem> problemList)
{undefined
List<Unit> unitList = new List<Unit>();
int[] eachTypeCount = paper.EachTypeCount;
Unit unit;
Random rand = new Random();
for (int i = 0; i < count; i++)
{undefined
unit = new Unit();
unit.ID = i + 1;
unit.AdaptationDegree = 0.00;
//总分限制
while (paper.TotalScore != unit.SumScore)
{undefined
unit.ProblemList.Clear();
//各题型题目数量限制
for (int j = 0; j < eachTypeCount.Length; j++)
{undefined
List<Problem> oneTypeProblem = problemList
.Where(o => o.Type == (j + 1))
.Where(p => IsContain(paper, p))
.ToList();
Problem temp = new Problem();
for (int k = 0; k < eachTypeCount[j]; k++)
{undefined
//选择不重复的题目
int index = rand.Next(0, oneTypeProblem.Count - k);
unit.ProblemList.Add(oneTypeProblem[index]);
temp = oneTypeProblem[oneTypeProblem.Count - 1 - k];
oneTypeProblem[oneTypeProblem.Count - 1 - k] = oneTypeProblem[index];
oneTypeProblem[index] = temp;
}
}
}
unitList.Add(unit);
}
//计算知识点覆盖率及适应度
unitList = GetKPCoverage(unitList, paper);
unitList = GetAdaptationDegree(unitList, paper, kpcoverage, difficulty);
return unitList;
}

2、计算种群个体的适应度

在上面的代码中最后调用了两个方法，GetKPCoverage跟GetAdaptationDegree，这两个方法分别是计算种群中个体的知识点覆盖率跟适应度。关于种群个体的知识点覆盖率在上一篇文章中已经说过了（知识点分布用一个个体知识点的覆盖率来衡量，例如期望本试卷包含N个知识点，而一个个体中所有题目知识点的并集中包含M个（M<=N），则知识点的覆盖率为M/N。），具体算法如下：

/// <summary>
/// 计算知识点覆盖率
/// </summary>
/// <param name="unitList">种群</param>
/// <param name="paper">期望试卷</param>
/// <returns>List</returns>
public List<Unit> GetKPCoverage(List<Unit> unitList, Paper paper)
{undefined
List<int> kp;
for (int i = 0; i < unitList.Count; i++)
{undefined
kp = new List<int>();
unitList[i].ProblemList.ForEach(delegate(Problem p)
{undefined
kp.AddRange(p.Points);
});
//个体所有题目知识点并集跟期望试卷知识点交集
var common = kp.Intersect(paper.Points);
unitList[i].KPCoverage = common.Count() * 1.00 / paper.Points.Count;
}
return unitList;
}

适应度方法的确定上一篇文章里已经说过，即：

<font style="color:rgb(77, 77, 77);">f=1-(1-M/N)*f1-|EP-P|*f2 </font>

其中M/N为知识点覆盖率，EP为期望难度系数，P为种群个体难度系数，f1为知识点分布的权重，f2为难度系数所占权重。当f1=0时退化为只限制试题难度系数，当f2=0时退化为只限制知识点分布。实现代码如下：

/// <summary>
/// 计算种群适应度
/// </summary>
/// <param name="unitList">种群</param>
/// <param name="paper">期望试卷</param>
/// <param name="KPCoverage">知识点分布在适应度计算中所占权重</param>
/// <param name="Difficulty">试卷难度系数在适应度计算中所占权重</param>
/// <returns>List</returns>
public List<Unit> GetAdaptationDegree(List<Unit> unitList, Paper paper, double KPCoverage, double Difficulty)
{undefined
unitList = GetKPCoverage(unitList, paper);
for (int i = 0; i < unitList.Count; i++)
{undefined
unitList[i].AdaptationDegree = 1 - (1 - unitList[i].KPCoverage) * KPCoverage - Math.Abs(unitList[i].Difficulty - paper.Difficulty) * Difficulty;
}
return unitList;
}

3、选择算子

这里选择算子采用轮盘赌选择法，即适应度越大的被选择到的概率越大。比如说种群中有20个个体，那么每个个体的适应度除以20个个体适应度的和得到的就是该个体的被选择的概率。轮盘赌选择时，每个个体类似于轮盘中的一小块扇形，扇形的大小与该个体被选择的概率成正比。那么，扇形越大的个体被选择的概率越大。这就是轮盘赌选择法。算法实现代码如下：

/// <summary>
/// 选择算子（轮盘赌选择）
/// </summary>
/// <param name="unitList">种群</param>
/// <param name="count">选择次数</param>
/// <returns>进入下一代的种群</returns>
public List<Unit> Select(List<Unit> unitList, int count)
{undefined
List<Unit> selectedUnitList = new List<Unit>();
//种群个体适应度和
double AllAdaptationDegree = 0;
unitList.ForEach(delegate(Unit u)
{undefined
AllAdaptationDegree += u.AdaptationDegree;
});
Random rand = new Random();
while (selectedUnitList.Count != count)
{undefined
//选择一个0—1的随机数字
double degree = 0.00;
double randDegree = rand.Next(1, 100) * 0.01 * AllAdaptationDegree;
//选择符合要求的个体
for (int j = 0; j < unitList.Count; j++)
{undefined
degree += unitList[j].AdaptationDegree;
if (degree >= randDegree)
{undefined
//不重复选择
if (!selectedUnitList.Contains(unitList[j]))
{undefined
selectedUnitList.Add(unitList[j]);
}
break;
}
}
}
return selectedUnitList;
}

4、交叉算子

交叉算子在上一篇也做了说明，写程序时为方便略做了一点更改，即把多点交叉改为单点交叉。在交叉过程在有几个地方需要注意，一是要保正总分不变，二是保证交叉后没有重复个体，算法实现如下：

/// <summary>
/// 交叉算子
/// </summary>
/// <param name="unitList">种群</param>
/// <param name="count">交叉后产生的新种群个体数量</param>
/// <param name="paper">期望试卷</param>
/// <returns>List</returns>
public List<Unit> Cross(List<Unit> unitList, int count, Paper paper)
{undefined
List<Unit> crossedUnitList = new List<Unit>();
Random rand = new Random();
while (crossedUnitList.Count != count)
{undefined
//随机选择两个个体
int indexOne = rand.Next(0, unitList.Count);
int indexTwo = rand.Next(0, unitList.Count);
Unit unitOne;
Unit unitTwo;
if (indexOne != indexTwo)
{undefined
unitOne = unitList[indexOne];
unitTwo = unitList[indexTwo];
//随机选择一个交叉位置
int crossPosition = rand.Next(0, unitOne.ProblemCount - 2);
//保证交叉的题目分数合相同
double scoreOne = unitOne.ProblemList[crossPosition].Score + unitOne.ProblemList[crossPosition + 1].Score;
double scoreTwo = unitTwo.ProblemList[crossPosition].Score + unitTwo.ProblemList[crossPosition + 1].Score;
if (scoreOne == scoreTwo)
{undefined
//两个新个体
Unit unitNewOne = new Unit();
unitNewOne.ProblemList.AddRange(unitOne.ProblemList);
Unit unitNewTwo = new Unit();
unitNewTwo.ProblemList.AddRange(unitTwo.ProblemList);
//交换交叉位置后面两道题
for (int i = crossPosition; i < crossPosition + 2; i++)
{undefined
unitNewOne.ProblemList[i] = new Problem(unitTwo.ProblemList[i]);
unitNewTwo.ProblemList[i] = new Problem(unitOne.ProblemList[i]);
}
//添加到新种群集合中
unitNewOne.ID = crossedUnitList.Count;
unitNewTwo.ID = unitNewOne.ID + 1;
if (crossedUnitList.Count < count)
{undefined
crossedUnitList.Add(unitNewOne);
}
if (crossedUnitList.Count < count)
{undefined
crossedUnitList.Add(unitNewTwo);
}
}
}
//过滤重复个体
crossedUnitList = crossedUnitList.Distinct(new ProblemComparer()).ToList();
}
//计算知识点覆盖率及适应度
crossedUnitList = GetKPCoverage(crossedUnitList, paper);
crossedUnitList = GetAdaptationDegree(crossedUnitList, paper, kpcoverage, difficulty);
return crossedUnitList;
}

上面过滤重复个体中用到了ProblemComparer类，这是一个自定义的比较类，代码如下：

public class ProblemComparer : IEqualityComparer<Unit>
{undefined
public bool Equals(Unit x, Unit y)
{undefined
bool result = true;
for (int i = 0; i < x.ProblemList.Count; i++)
{undefined
if (x.ProblemList[i].ID != y.ProblemList[i].ID)
{undefined
result = false;
break;
}
}
return result;
}
public int GetHashCode(Unit obj)
{undefined
return obj.ToString().GetHashCode();
}
}

5、变异算子

在变异过程中主要是要保证替换题目至少包含一个被替换题的有效知识点（期望试卷中也包含此知识点），并要类型相同，分数相同而题号不同。算法实现代码如下：

/// <summary>
/// 变异算子
/// </summary>
/// <param name="unitList">种群</param>
/// <param name="problemList">题库</param>
/// <param name="paper">期望试卷</param>
/// <returns>List</returns>
public List<Unit> Change(List<Unit> unitList, List<Problem> problemList, Paper paper)
{undefined
Random rand = new Random();
int index = 0;
unitList.ForEach(delegate(Unit u)
{undefined
//随机选择一道题
index = rand.Next(0, u.ProblemList.Count);
Problem temp = u.ProblemList[index];
//得到这道题的知识点
Problem problem = new Problem();
for (int i = 0; i < temp.Points.Count; i++)
{undefined
if (paper.Points.Contains(temp.Points[i]))
{undefined
problem.Points.Add(temp.Points[i]);
}
}
//从数据库中选择包含此题有效知识点的同类型同分数不同题号试题
var otherDB = from a in problemList
where a.Points.Intersect(problem.Points).Count() > 0
select a;
List<Problem> smallDB = otherDB.Where(p => IsContain(paper, p)).Where(o => o.Score == temp.Score && o.Type == temp.Type && o.ID != temp.ID).ToList();
//从符合要求的试题中随机选一题替换
if (smallDB.Count > 0)
{undefined
int changeIndex = rand.Next(0, smallDB.Count);
u.ProblemList[index] = smallDB[changeIndex];
}
});
//计算知识点覆盖率跟适应度
unitList = GetKPCoverage(unitList, paper);
unitList = GetAdaptationDegree(unitList, paper, kpcoverage, difficulty);
return unitList;
}

6、调用示例

遗传算法主要算法上面都已实现，现在就是调用了。调用过程按如下流程图进行：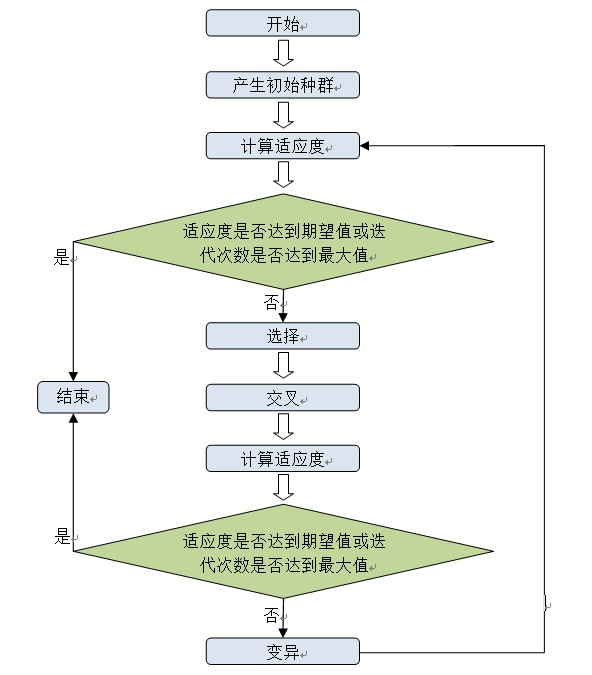

基于遗传算法实现自动组卷 - 图4

基于遗传算法的自动组卷系统流程图这里初始种群大小设定为20，最大迭代次数为500，适应度为0.98，选择算子选择次数为10次，交叉算子产生的个体数量为20，期望试卷难度系数为0.72，总分为100分，各种题型题数为：20（单选）, 5（多选）, 10（判断）, 7（填空）, 5（问答），包含的知识点为：1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 55, 57, 59, 61, 63, 65, 67, 69, 71, 73, 75, 77, 79, 81。代码如下：

/// <summary>
/// 调用示例
/// </summary>
public void Show()
{undefined
//题库
DB db = new DB();
//期望试卷
Paper paper = new Paper()
{undefined
ID = 1,
TotalScore = 100,
Difficulty = 0.72,
Points = new List<int>() { 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 55, 57, 59, 61, 63, 65, 67, 69, 71, 73, 75, 77, 79, 81 },
EachTypeCount = new[] { 20, 5, 10, 7, 5 }
};
//迭代次数计数器
int count = 1;
//适应度期望值
double expand = 0.98;
//最大迭代次数
int runCount = 500;
//初始化种群
List<Unit> unitList = CSZQ(20, paper, db.ProblemDB);
Console.WriteLine("\n\n      -------遗传算法组卷系统(http://www.cnblogs.com/durongjian/)---------\n\n");
Console.WriteLine("初始种群：");
ShowUnit(unitList);
Console.WriteLine("-----------------------迭代开始------------------------");
//开始迭代
while (!IsEnd(unitList, expand))
{undefined
Console.WriteLine("在第 " + (count++) + " 代未得到结果");
if (count > runCount)
{undefined
Console.WriteLine("计算 " + runCount + " 代仍没有结果，请重新设计条件！");
break;
}
//选择
unitList = Select(unitList, 10);
//交叉
unitList = Cross(unitList, 20, paper);
//是否可以结束（有符合要求试卷即可结束）
if (IsEnd(unitList, expand))
{undefined
break;
}
//变异
unitList = Change(unitList, db.ProblemDB, paper);
}
if (count <= runCount)
{undefined
Console.WriteLine("在第 " + count + " 代得到结果，结果为：\n");
Console.WriteLine("期望试卷难度：" + paper.Difficulty + "\n");
ShowResult(unitList, expand);
}
}

最后在控制台中调用此方法即可。

7、其他辅助方法

在上面的代码中还调用了几个辅助方法，下面一并给出：

#region 是否达到目标
/// <summary>
/// 是否达到目标
/// </summary>
/// <param name="unitList">种群</param>
/// <param name="endcondition">结束条件（适应度要求）</param>
/// <returns>bool</returns>
public bool IsEnd(List<Unit> unitList, double endcondition)
{undefined
if (unitList.Count > 0)
{undefined
for (int i = 0; i < unitList.Count; i++)
{undefined
if (unitList[i].AdaptationDegree >= endcondition)
{undefined
return true;
}
}
}
return false;
}
#endregion
#region 显示结果
/// <summary>
/// 显示结果
/// </summary>
/// <param name="unitList">种群</param>
/// <param name="expand">期望适应度</param>
public void ShowResult(List<Unit> unitList, double expand)
{undefined
unitList.OrderBy(o => o.ID).ToList().ForEach(delegate(Unit u)
{undefined
if (u.AdaptationDegree >= expand)
{undefined
Console.WriteLine("第" + u.ID + "套：");
Console.WriteLine("题目数量\t知识点分布\t难度系数\t适应度");
Console.WriteLine(u.ProblemCount + "\t\t" + u.KPCoverage.ToString("f2") + "\t\t" + u.Difficulty.ToString("f2") + "\t\t" + u.AdaptationDegree.ToString("f2")+"\n\n");
}
});
}
#endregion
#region 显示种群个体题目编号
/// <summary>
/// 显示种群个体题目编号
/// </summary>
/// <param name="u">种群个体</param>
public void ShowUnit(Unit u)
{undefined
Console.WriteLine("编号\t知识点分布\t难度系数");
Console.WriteLine(u.ID + "\t" + u.KPCoverage.ToString("f2") + "\t\t" + u.Difficulty.ToString("f2"));
u.ProblemList.ForEach(delegate(Problem p)
{undefined
Console.Write(p.ID + "\t");
});
Console.WriteLine();
}
#endregion

#region 题目知识点是否符合试卷要求
/// <summary>
/// 题目知识点是否符合试卷要求
/// </summary>
/// <param name="paper">期望试卷</param>
/// <param name="problem">一首试题</param>
/// <returns>bool</returns>
private bool IsContain(Paper paper, Problem problem)
{undefined
for (int i = 0; i < problem.Points.Count; i++)
{undefined
if (paper.Points.Contains(problem.Points[i]))
{undefined
return true;
}
}
return false;
}
#endregion

基于遗传算法实现自动组卷