排序算法

以从小到大排序为例子

冒泡排序

比较相邻连个元素之间的大小，如果前面的比后面的大就交换位置

function bubbleSort(arr) {
  console.log('%c ----开始排序-----', 'background-color: green; color: white')
  const len = arr.length;
  for(let i = 0; i < len - 1; i++) {
    console.log(`i=${i}        ##%c ${arr.join(', ')}`, 'color: red')
    for(let j = 0; j < len - 1 - i; j++) {
      if (arr[j] > arr[j+1]) {
        [arr[j], arr[j+1]] = [arr[j+1], arr[j]]
      }
      console.log(`  i=${i}, j=${j} ##%c ${arr.join(', ')}`, 'color: red')
    }
  }
  console.log('%c ----排序完成-----', 'background-color: green; color: white')
  return arr;
}
var arr = [6, 5, 8, 7, 2, 0, 3, 1, 4, 9]
console.log('排序前：', arr.join(', '))
console.log('排序后：', bubbleSort(arr).join(', '))

冒泡排序第1次遍历后会将最大值放到最右边，这个最大值也是全局最大值。
_
假如从开始的第一对到结尾的最后一对，相邻的元素之间都没有发生交换的操作，这意味着右边的元素总是大于等于左边的元素，此时的数组已经是有序的了，我们无需再对剩余的元素重复比较下去了。

function bubbleSortOptimization(arr) {
  if (arr.length < 2) return arr;
  console.log('%c ----开始排序-----', 'background-color: green; color: white')
  const len = arr.length;
  for(let i = 0; i < len - 1; i++) {
    console.log(`i=${i}        ##%c ${arr.join(', ')}`, 'color: red')
    let flag = false
    for(let j = 0; j < len - 1 - i; j++) {
      if (arr[j] > arr[j+1]) {
        [arr[j], arr[j+1]] = [arr[j+1], arr[j]]
        flag = true;
      }
      console.log(`  i=${i}, j=${j} ##%c ${arr.join(', ')}`, 'color: red')
    }
    if (!flag) {
      console.log('一轮下来没有发上交换，说明数组已经是有序的了，直接结束掉')
      break;
    }
  }
  console.log('%c ----排序完成-----', 'background-color: green; color: white')
  return arr;
}
var arr = [6, 5, 8, 7, 2, 0, 3, 1, 4, 9]
console.log('排序前：', arr.join(', '))
console.log('排序后：', bubbleSortOptimization(arr).join(', '))

选择排序

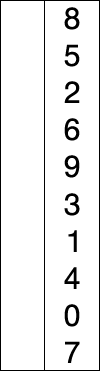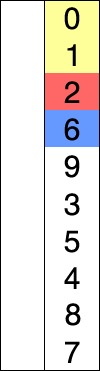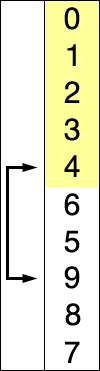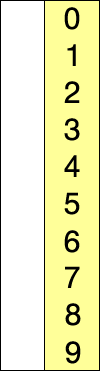
首先，找到数组中最小的那个元素，
其次，将它和数组的第一个元素交换位置(如果第一个元素就是最小元素那么它就和自己交换)。
然后，在剩下的元素中找到最小的元素，将它与数组的第二个元素交换位置。如此往复，直到将整个数组排序。这种方法我们称之为选择排序。

function selectSort (arr) {
  if (arr.length < 2) return arr;
  console.log('%c ----开始排序-----', 'background-color: green; color: white')
  const len = arr.length;
  for(let i = 0; i < len - 1; i++) {
    let index = i
      for(let j = i + 1; j < len; j++) {
        if (arr[index] > arr[j]) {
        index = j
            }
    }
    [arr[index], arr[i]]= [arr[i], arr[index]];
    console.log(`${i + 1}轮结果:  ##%c ${arr.join(', ')}`, 'color: red')
  }
  console.log('%c ----排序完成-----', 'background-color: green; color: white')
  return arr
}
var arr = [6, 5, 8, 7, 2, 0, 3, 1, 4, 9]
console.log('排序前：', arr.join(', '))
console.log('排序后：', selectSort(arr).join(', '))

插入排序

我们在玩打牌的时候，你是怎么整理那些牌的呢？一种简单的方法就是一张一张的来，将每一张牌插入到其他已经有序的牌中的适当位置。当我们给无序数组做排序的时候，为了要插入元素，我们需要腾出空间，将其余所有元素在插入之前都向右移动一位，这种算法我们称之为插入排序。

• 左边是有序区，右边是无序去
• 依次拿无序去的每一个元素与有序区进行比较（从右往左比较），找到一个合适的位置（左边的元素比他小右边的元素比他大），插进去

function insertSort (arr) {
  let len = arr.length
  if (len < 2) return arr
  for(let i = 1; i < len; i++) {
    let temp = arr[i]
    let k = i - 1;
    while (k >= 0 && arr[k] > temp) { // k就是temp要插入的位置
        k--;
    }
      // 腾挪位置插入
      for(let j = i; j > k + 1; j--) {
        arr[j] = arr[j - 1]
    }
    arr[k + 1] = temp
  }
  return arr
}
var arr = [6, 5, 8, 7, 2, 0, 3, 1, 4, 9]
console.log('排序前：', arr.join(', '))
console.log('排序后：', insertSort(arr).join(', '))

**

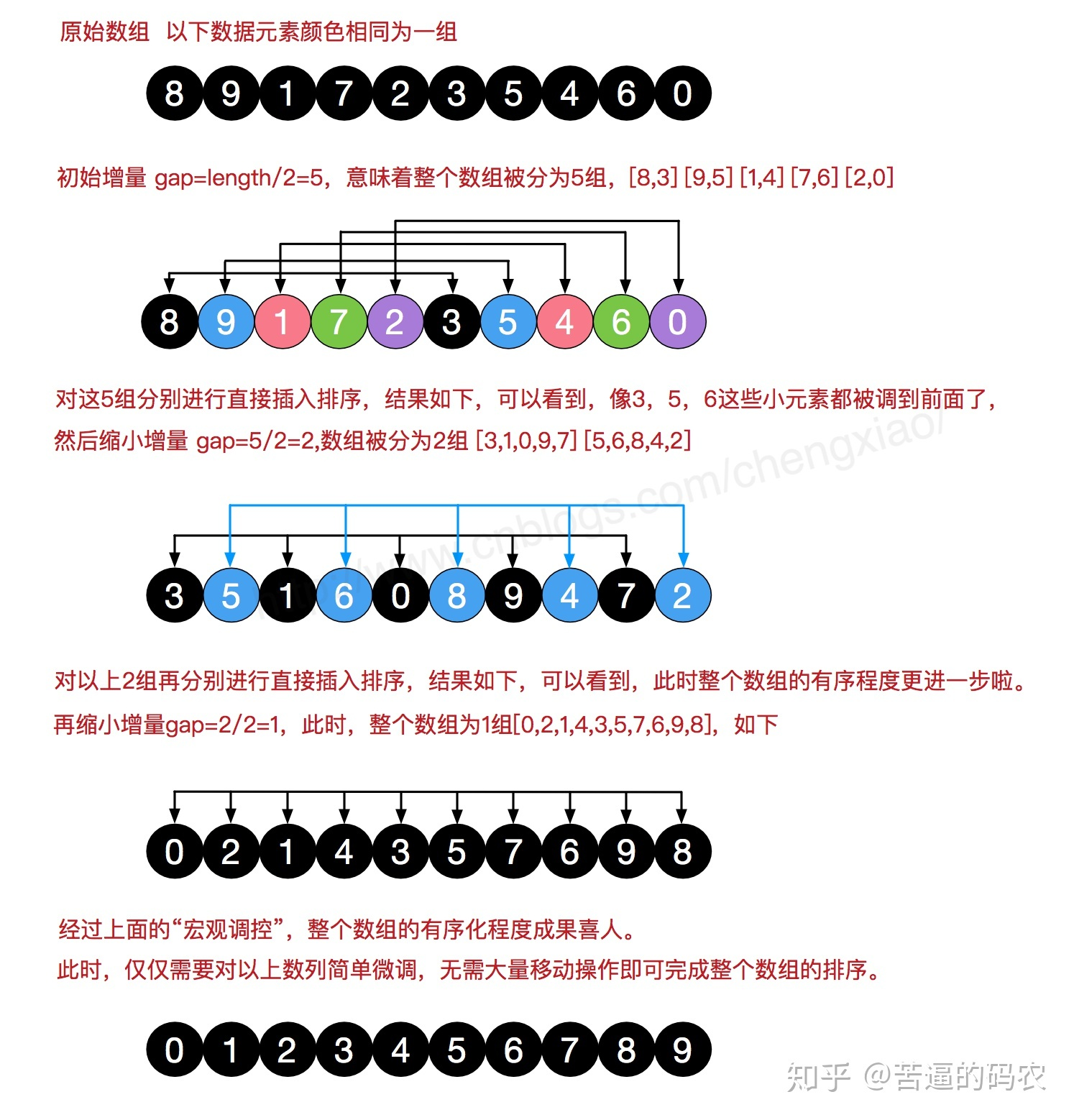
希尔排序

希尔排序可以说是插入排序的一种变种。无论是插入排序还是冒泡排序，如果数组的最大值刚好是在第一位，要将它挪到正确的位置就需要 n - 1 次移动。也就是说，原数组的一个元素如果距离它正确的位置很远的话，则需要与相邻元素交换很多次才能到达正确的位置，这样是相对比较花时间了。

利用二分法的思想优化插入排序

function shellSort(arr) {
  let len = arr.length;
  if (len < 2) return arr
  let gap = 1
  while (gap < len / 3) {          // 动态定义间隔序列
    gap = gap * 3 + 1;  
  }
  //上面是设置动态增量算法
  //下面是其实是插入排序 和 冒泡排序交换位置
  while (gap >= 1) {
    for (let i = 0; i < len; i++) {      //插入排序
      for (let j = i; j >= gap && arr[j] < arr[j - gap]; j -= gap) {
        [arr[j- gap], arr[j]] = [arr[j], arr[j- gap]]
      }
    }
    gap = (gap-1)/3;
  }
  return arr
}
console.log(shellSort([84, 83, 88, 87,61,50, 70,60,80,99]).join(', '))
// 交换法，性能比插入排序还差
function shellSort2 (arr) {
  let len = arr.length;
  if (len < 2) return arr;
  let count = 0; // 第几轮
  for (let gap = Math.floor(len / 2); gap > 0; gap = Math.floor(gap / 2)) {
    for (let i = gap; i < len; i++) {
        for(let j = i - gap; j >= 0; j -= gap) {
        if (arr[j] > arr[j + gap]) {
          [arr[j], arr[j + gap]] = [arr[j + gap], arr[j]]
        }
      }
    }
    count ++;
    console.log(`第${count}轮： ${arr.join(', ')}`)
  }
  return arr
}
console.log(shellSort2([8, 9, 1, 7, 5, 4, 6, 0]).join(', '))
// 移位法
function shellSort3 (arr) {
  let len = arr.length;
  if (len < 2) return arr;
  let count = 0;
  for (let gap = Math.floor(len / 2); gap > 0; gap = Math.floor(gap / 2)) {
    for (let i = gap; i < len; i++) {
      let j = i;
      let temp = arr[j]
      if (arr[j] < arr[j - gap]) {
        while (j >= gap && arr[j - gap] > temp) {
          arr[j] = arr[j - gap];
          j -= gap;
        }
        arr[j] = temp;
        arr[j] = temp
      }
    }
    count ++;
    console.log(`第${count}轮： ${arr.join(', ')}`)
  }
  return arr
}
console.log(shellSort3([8, 9, 1, 7, 5, 4, 6, 0]).join(', '))

归并排序

将一个大的无序数组有序，我们可以把大的数组分成两个，然后对这两个数组分别进行排序，之后在把这两个数组合并成一个有序的数组。由于两个小的数组都是有序的，所以在合并的时候是很快的。
通过递归的方式将大的数组一直分割，直到数组的大小为 1，此时只有一个元素，那么该数组就是有序的了，之后再把两个数组大小为1的合并成一个大小为2的，再把两个大小为2的合并成4的 ….. 直到全部小的数组合并起来。

// 作为一种典型的分而治之思想的算法应用，归并排序的实现由两种方法
function merge(left, right) { // 采用自上而下的递归
  const result = []
  while (left.length && right.length) {
    if (left[0] < right[0]) {
      result.push(left.shift())
    } else {
      result.push(right.shift())
    }
  }
  while (left.length) {
    result.push(left.shift())
  }
  while (right.length) {
    result.push(right.shift())
  }
  return result
}
function mergeSort (arr) {
  let len = arr.length
  if (len < 2) return arr
  let mid = Math.floor(len / 2)
  return merge(mergeSort(arr.slice(0, mid)), mergeSort(arr.slice(mid)))
}
console.log(mergeSort([6, 5, 8, 7, 2, 0, 3, 1, 4, 9]).join(', '))

快速排序

1. 以第一个元素为基准，后面的数依次和它比较，最后剩下的数分成两组，一组比它大，一组比它小
2. 现在就可以认为这个基准数在有序的位置了，那么他的左边和右边分别按照步骤一进行比较
3. 如果数组长度为0或1就不在比较，所有分组运行完成，排序就结束了

function quickSort (arr, left, right) {
  const len = arr.length
  if(len < 2) return arr
  if(left === undefined) left = 0
  if(right === undefined) right = arr.length
  if(left < right) {
    const midIndex = patition(arr, left, right)
    quickSort(arr, left, midIndex - 1)
    quickSort(arr, midIndex + 1, right)
  }
  return arr
}
// 理解快速排序，关键在第一步，如何划分区间的
function patition (arr, left, right) {
  let pivot = left      // 分区操作
  let index = pivot + 1 // 设定基准值（pivot）
  for(let i = index; i <= right; i++) {
    if(arr[pivot] > arr[i]) {
      ;[arr[index], arr[i]] = [arr[i], arr[index]];
      index++
    }
  }
  [arr[index - 1], arr[pivot]] = [arr[pivot], arr[index - 1]]
  return index - 1
}
console.log('quickSort', quickSort([6, 5, 8, 7, 2, 0, 3, 1, 4, 9]).join(', '))

计数排序

分布式排序使用已组织好的辅助数据结构(称为桶), 然后进行合并，得到排好序的数组。计数排序使用-一个用来存储每个元素在原始数组中出现次数的临时数组。在所有元素都计数完成后，临时数组已排好序并可迭代以构建排序后的结果数组。
计数排序不是基于比较的排序算法，其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。

􏽔􏰁􏻴􏱨􏱩􏴄􏱪􏱫􏸓􏱽􏱱􏱯􏱩􏰜􏳰􏿢􏴼􏱽􏱱􏲚􏳐􏰚􏳻􏰪􏱆􏱇􏳰􏱫􏰤􏰥􏰦􏰜􏱨􏳭􏲧􏰦􏰻􏱚􏱯􏰚 􏵏􏰝􏰞􏰶􏱘􏵷􏵸􏰦􏱽􏱱􏲚􏳐􏰚􏲂􏲠􏹡􏵁􏱽􏱱􏱨􏰞􏱬􏱽􏱱􏲧􏰻􏱚􏰦􏰤􏻆􏰦􏲚􏳐􏱯􏰚􏱬􏲹􏳈􏱘􏰜􏰡􏳃 􏱽􏱱􏰕􏴁􏰠􏰚􏳻􏰪􏴌􏱰􏰦􏰜􏰹􏱷􏱫􏰽􏳒􏰻􏱚􏰕􏽔􏰁􏻴􏱨􏱩􏴄􏱪􏱫􏸓􏱽􏱱􏱯􏱩􏰜􏳰􏿢􏴼􏱽􏱱􏲚􏳐􏰚􏳻􏰪􏱆􏱇􏳰􏱫􏰤􏰥􏰦􏰜􏱨􏳭􏲧􏰦􏰻􏱚􏱯􏰚 􏵏􏰝􏰞􏰶􏱘􏵷􏵸􏰦􏱽􏱱􏲚􏳐􏰚􏲂􏲠􏹡􏵁􏱽􏱱􏱨􏰞􏱬􏱽􏱱􏲧􏰻􏱚􏰦􏰤􏻆􏰦􏲚􏳐􏱯􏰚􏱬􏲹􏳈􏱘􏰜􏰡􏳃 􏱽􏱱􏰕􏴁􏰠􏰚􏳻􏰪􏴌􏱰􏰦􏰜􏰹􏱷􏱫􏰽􏳒􏰻􏱚􏰕

function countingSort(array) {
  if (array.length < 2) {
    return array;
  }
  const maxValue = findMaxValue(array);
  let sortedIndex = 0;
  const counts = new Array(maxValue + 1);
  array.forEach(element => {
    if (!counts[element]) {
      counts[element] = 0;
    }
    counts[element]++;
  });
  // console.log('Frequencies: ' + counts.join());
  //forEach 方法按升序为数组中含有效值的每一项执行一次callback 函数，那些已删除（使用delete方法等情况）或者未初始化的项将被跳过（但不包括那些值为 undefined 的项）（例如在稀疏数组上）
  // key 为 负数 不会遍历
  counts.forEach((element, i) => {
    while (element > 0) {
      array[sortedIndex++] = i;
      element--;
    }
  });
  return array;
}

桶排序

桶排序是计数排序的升级版。它利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。桶排序 (Bucket sort)的工作的原理：假设输入数据服从均匀分布，将数据分到有限数量的桶里，每个桶再分别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排）。

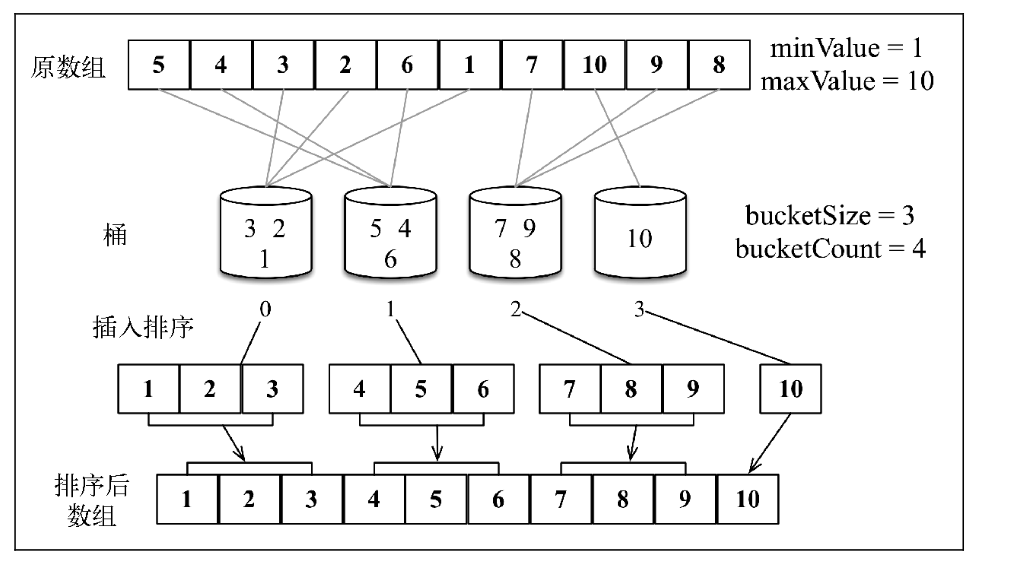
function createBuckets(array, bucketSize) {
  let minValue = array[0];
  let maxValue = array[0];
  for (let i = 1; i < array.length; i++) {
    if (array[i] < minValue) {
      minValue = array[i];
    } else if (array[i] > maxValue) {
      maxValue = array[i];
    }
  }
  const bucketCount = Math.floor((maxValue - minValue) / bucketSize) + 1;
  const buckets = [];
  for (let i = 0; i < bucketCount; i++) {
    buckets[i] = [];
  }
  for (let i = 0; i < array.length; i++) {
    buckets[Math.floor((array[i] - minValue) / bucketSize)].push(array[i]);
  }
  return buckets;
}
function sortBuckets(buckets) {
  const sortedArray = [];
  for (let i = 0; i < buckets.length; i++) {
    if (buckets[i] != null) {
      insertionSort(buckets[i]); // 调用插入排序
      sortedArray.push(...buckets[i]);
    }
  }
  return sortedArray;
}
function bucketSort(array, bucketSize = 5) {
  if (array.length < 2) {
    return array;
  }
  const buckets = createBuckets(array, bucketSize);
  return sortBuckets(buckets);
}

基数排序

基数排序也是-个分布式排序算法，它根据数字的有效位或基数(这也是它为什么叫基数排序)将整数分布到桶中。基数是基于数组中值的记数制的。
使用空间换时间的经典算法

const getBucketIndex = (value, minValue, significantDigit, radixBase) =>
  Math.floor(((value - minValue) / significantDigit) % radixBase);
const countingSortForRadix = (array, radixBase, significantDigit, minValue) => {
  let bucketsIndex;
  const buckets = [];
  const aux = [];
  for (let i = 0; i < radixBase; i++) {
    buckets[i] = 0;
  }
  for (let i = 0; i < array.length; i++) {
    bucketsIndex = getBucketIndex(array[i], minValue, significantDigit, radixBase);
    buckets[bucketsIndex]++;
  }
  for (let i = 1; i < radixBase; i++) {
    buckets[i] += buckets[i - 1];
  }
  for (let i = array.length - 1; i >= 0; i--) {
    bucketsIndex = getBucketIndex(array[i], minValue, significantDigit, radixBase);
    aux[--buckets[bucketsIndex]] = array[i];
  }
  for (let i = 0; i < array.length; i++) {
    array[i] = aux[i];
  }
  return array;
};
function radixSort(array, radixBase = 10) {
  if (array.length < 2) {
    return array;
  }
  let minValue = array[0];
  let maxValue = array[0];
  for (let i = 1; i < array.length; i++) {
    if (minValue > array[i]) {
      minValue = array[i];
    }
    if (maxValue < array[i]) {
      maxValue = array[i];
    }
  }
  // Perform counting sort for each significant digit, starting at 1
  let significantDigit = 1;
  while ((maxValue - minValue) / significantDigit >= 1) {
    // console.log('radix sort for digit ' + significantDigit);
    array = countingSortForRadix(array, radixBase, significantDigit, minValue);
    // console.log(array.join());
    significantDigit *= radixBase;
  }
  return array;
}
console.log(radixSort([456, 789, 123, 1, 32, 4, 243, 321, 42, 90, 10, 999]))

堆排序

我们可以使用二叉堆数据结构来帮助我们创建一个非常著名的排序算法:堆排序算法。它包
含下面三个步骤。

1. 用数组创建一个最大堆用作源数据。
2. 在创建最大堆后，最大的值会被存储在堆的第- - 个位置。我们要将它替换为堆的最后一个值，将堆的大小减1。
3. 最后，我们将堆的根节点下移并重复步骤2直到堆的大小为1。

我们用最大堆得到一个升序排列的数组( 从最小到最大)。如果我们想要这个数组按降序排
列，可以用最小堆代替。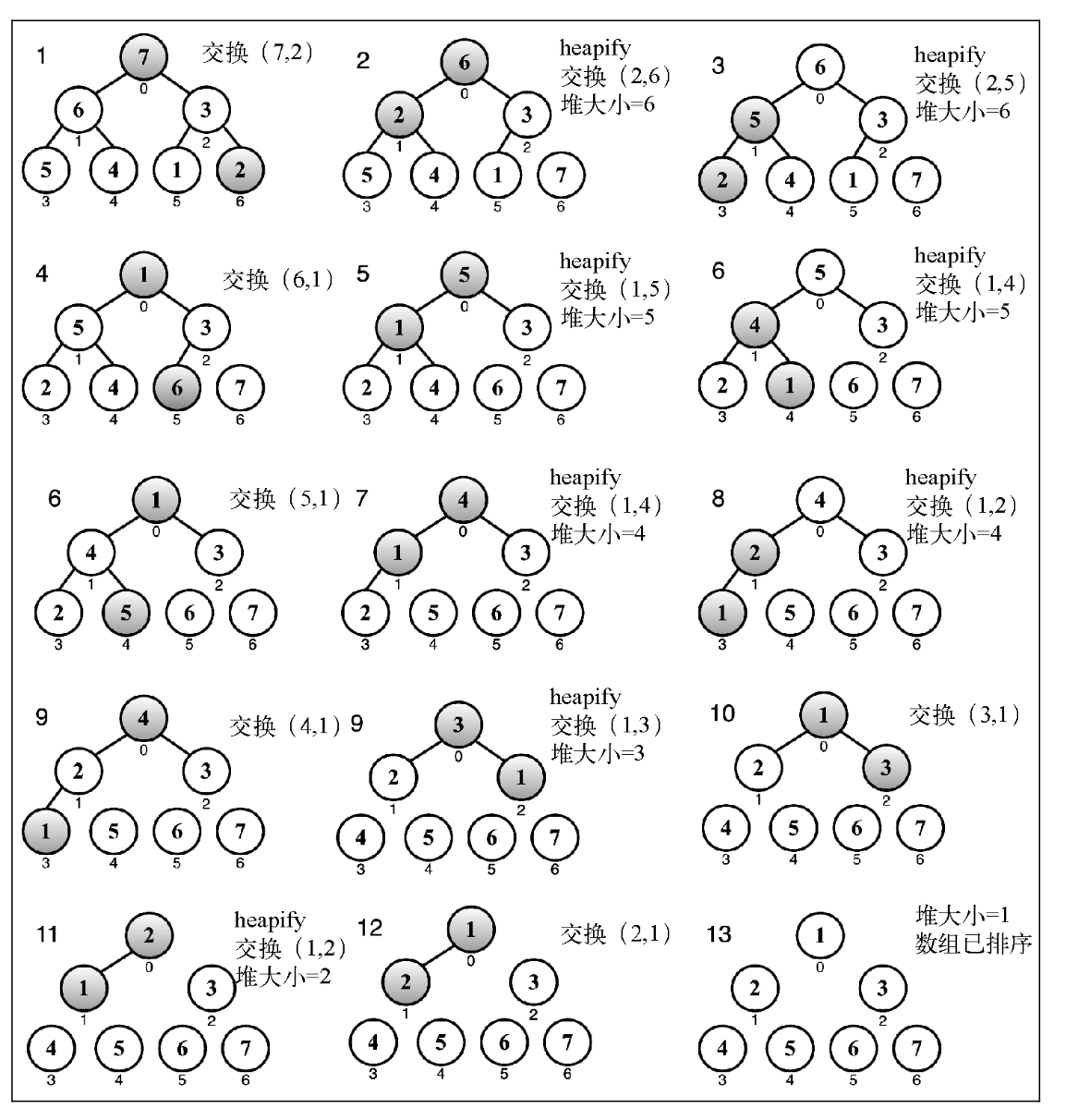

function heapSort(arr) {
  if(arr.length < 2) return arr
  let heapSize = arr.length
  buildMaxHeap(arr)
  while (heapSize > 1) {
    --heapSize;
    [arr[0], arr[heapSize]] = [arr[heapSize], arr[0]];
    heapify(arr, 0, heapSize)
  }
  return arr
}
function buildMaxHeap(arr) {
  const index = Math.floor(arr.length / 2)
  for(let i = index; i >= 0; i--) {
    heapify(arr, i, arr.length)
  }
}
function heapify(arr, index, heapSize) { // 最大堆平衡
  let maxNumIndex = index
  const left = 2*index + 1
  if(left < heapSize && arr[left] > arr[maxNumIndex]){
    maxNumIndex= left
  }
  const right = 2*index + 2
  if(right < heapSize && arr[right] > arr[maxNumIndex]){
    maxNumIndex= right
  }
  if(maxNumIndex !== index) {
    [arr[index], arr[maxNumIndex]] = [arr[maxNumIndex], arr[index]]
    heapify(arr, maxNumIndex, heapSize)
  }
}
console.log('heapSort', heapSort([6, 5, 8, 7, 2, 0, 3, 1, 4, 9]).join(', '))

Tim排序

https://v8.dev/blog/array-sort

其他

算法复杂度

Array.prototype.sort实现

• 没有回掉函数 是按照字符编码的顺序进行排序
• 各浏览器的算法实现

递归与递推

递推：从初值出发反复进行某一运算得到所需结果。——-从已知到未知，从小到大（比如每年长高9cm，20年180，30后270）
递归：从所需结果出发不断回溯前一运算直到回到初值再递推得到所需结果——从未知到已知，从大到小，再从小到大(你想进bat，那么编程就的牛逼，就得卸载玩者农药，努力学习）。递归(Recursion)是从归纳法(Induction)衍生出来的。

// 以 斐波那契数列 为例
//递归求解
function fib(n){
    return n <2 ? 1 : fib(n - 1) + fib(n - 2);
} 
//递推求解
function fib(n) {
    let start = 0;
    let fn = 1;
    for (let i = 0; i < n; i++) {
        let t = fn;
        fn = fn + start;
        start = t;
    }
    return fn;
}