红黑树是平衡二叉查找树的一种。为了深入理解红黑树，我们需要从二叉查找树开始讲起。

BST

二叉查找树（Binary Search Tree，简称BST）是一棵二叉树，它的左子节点的值比父节点的值要小，右节点的值要比父节点的值大。它的高度决定了它的查找效率。

在理想的情况下，二叉查找树增删查改的时间复杂度为O(logN)（其中N为节点数），最坏的情况下为O(N)。

BST存在倾斜的问题
平衡的BST：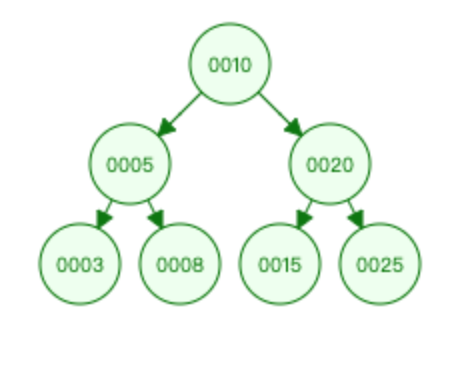
image.png

倾斜的BST:
image.png

  1. public class BstTest {
  3.     static class Node {
  4.         public String content;
  5.         public Node parent;
  6.         public Node left;
  7.         public Node right;
  9.         public Node(String content) {
  10.             this.content = content;
  11.         }
  12.     }
  14.     public Node root;
  16.     // BST的查找操作
  18.     public Node search (String content) {
  19.         Node r = root;
  20.         while (r != null) {
  21.             if (r.content.equals(content)) {
  22.                 return r;
  23.             } else if (content.compareTo(r.content) > 1) {
  24.                 r = r.right;
  25.             } else if (content.compareTo(r.content) <= 1) {
  26.                 r = r.left;
  27.             }
  28.         }
  30.         return null;
  31.     }
  33.     // BST的插入操作
  34.     public void insert (String content) {
  35.         Node newNode = new Node(content);
  36.         Node r = root;
  37.         Node parent = null;
  39.         if (r == null) {
  40.             root = newNode;
  41.             return;
  42.         }
  44.         while (r != null) {
  45.             parent = r;
  46.             if (newNode.content.compareTo(r.content) > 1) {
  47.                 r = r.right;
  48.             } else if (newNode.content.compareTo(r.content) < 1){
  49.                 r = r.left;
  50.             } else {
  51.                 r = r.left;
  52.             }
  53.         }
  55.         if (parent.content.compareTo(newNode.content) > 1) {
  56.             parent.left = newNode;
  57.             newNode.parent = parent;
  58.         } else {
  59.             parent.right = newNode;
  60.             newNode.parent = parent;
  61.         }
  62.     }
  63. }

红黑树-RBTree

基于BST存在的问题，一种新的树——平衡二叉查找树(Balanced BST)产生了。平衡树在插入和删除的时候，会通过旋转操作将高度保持在logN。其中两款具有代表性的平衡树分别为AVL树和红黑树。AVL树由于实现比较复杂，而且插入和删除性能差，在实际环境下的应用不如红黑树。

红黑树（Red-Black Tree，以下简称RBTree）的实际应用非常广泛，比如Linux内核中的完全公平调度器、高精度计时器、ext3文件系统等等，各种语言的函数库如Java的TreeMap和TreeSet，C++ STL的map、multimap、multiset等。

RBTree也是函数式语言中最常用的持久数据结构之一，在计算几何中也有重要作用。值得一提的是，Java 8中HashMap的实现也因为用RBTree取代链表，性能有所提升。

《算法导论》中对于红黑树的定义如下：

  1. 每个结点或是红的，或是黑的
  2. 根节点是黑的
  3. 每个叶结点是黑的
  4. 如果一个结点是红的，则它的两个儿子都是黑的
  5. 对每个结点，从该结点到其子孙节点的所有路径上包含相同数目的黑结点

对与第4点，网上有些定义是：父子节点之间不能出现两个连续的红节点，这种定义和《算法导论》中定义的效果是一样的

RBTree在理论上还是一棵BST树，但是它在对BST的插入和删除操作时会维持树的平衡，即保证树的高度在[logN,logN+1]（理论上，极端的情况下可以出现RBTree的高度达到2*logN，但实际上很难遇到）。这样RBTree的查找时间复杂度始终保持在O(logN)从而接近于理想的BST。RBTree的删除和插入操作的时间复杂度也是O(logN)。RBTree的查找操作就是BST的查找操作。

插入数据

向红黑树中插入新的结点。具体做法是，将新结点的 color 赋为红色，然后以BST的插入方法插入到红黑树中去。之所以将新插入的结点的颜色赋为红色，是因为：如果设为黑色，就会导致根到叶子的路径上有一条路上，多一个额外的黑结点，这个是很难调整的。但是设为红色结点后，可能会导致出现两个连续红色结点的冲突，那么可以通过颜色调换和树旋转来调整，这样简单多了。

接下来，讨论一下插入以后，红黑树的情况。设要插入的结点为N，其父结点为P，其 祖父结点为G，其父亲的兄弟结点为U（即P和U 是同一个结点的两个子结点）。如果P是黑色的，则整棵树不必调整就已经满足了红黑树的所有性质。如果P是红色的（可知，其父结点G一定是黑色的），则插入N后，违背了红色结点只能有黑色孩子的性质，需要进行调整。

调整时分以下三种情况：

新结点N的叔叔结点U是红色的

处理方式是：将P和U修改为黑色，G修改为红色。

现在新结点N有了一个黑色的父结点P，因为通过父结点P或叔父结点U的任何路径都必定通过祖父结点G，在这些路径上的黑结点数目没有改变。

但是，红色的祖父结点G的父结点也有可能是红色的，这就违反了性质3。为了解决这个问题，我们从祖父结点G开始递归向上调整颜色。如图2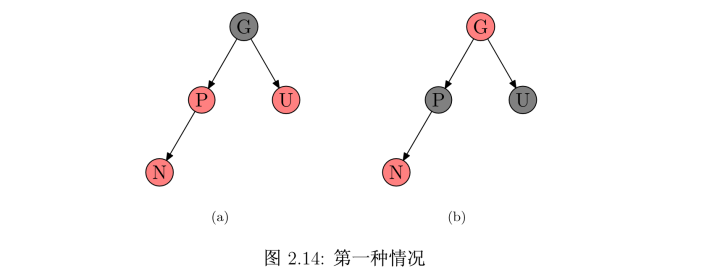红黑树笔记 - 图3

新结点N的叔叔结点U是黑色的，且N是左孩子。

处理方式：对祖父结点G进行一次右旋转

在旋转后产生的树中，以前的父结点P现在是新结点N和以前的祖父节点G的父结点，然后交换以前的父结点P和祖父结点G的颜色，结果仍满足红黑树性质。如图 2.15。在(b)中，虚线代表原来的指针，实线代表旋转过后的指针。所谓旋转就是改变图中所示的两个指针的值即可。当然，在实际应用中，还有父指针p也需要修改，这里为了图示的简洁而省略掉了。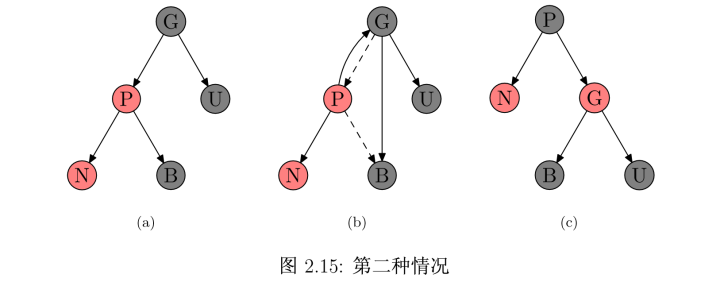
红黑树笔记 - 图4

新结点N的叔叔结点U是黑色的，且N是右孩子。

处理方式：对P进行一次左旋转，就把问题转化成了第二种情况。如图 2.16所示。
红黑树笔记 - 图5

红黑树插入数据的代码与二叉查找树是相同的，只是在插入以后，会对不满足红黑树性质的结点进行调整。

HashMap中红黑树的插入操作

  1. static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,
  2.                                             TreeNode<K,V> x) {
  3.     // 新节点默认为红色
  4.     x.red = true;
  5.     // xp表示x的父结点，xpp表示x的祖父结点，xppl表示xpp的左孩子结点，xppr表示xpp的右孩子结点
  6.     for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {
  7.         // 如果x没有父结点，则表示x是第一个结点，自动为根节点，根节点为黑色
  8.         if ((xp = x.parent) == null) {
  9.             x.red = false;
  10.             return x;
  11.         }
  12.         // 如果父结点不是红色（就是黑色），或者x没有祖父节点，那么就证明x是第二层节点，父节点为根节点
  13.         // 这种情况无需就行操作
  14.         else if (!xp.red || (xpp = xp.parent) == null)
  15.             return root;
  17.         // 进入到这里，表示x的父节点为红色
  19.         // 如果x的父节点是祖父结点的左孩子
  20.         if (xp == (xppl = xpp.left)) {
  21.             // 祖父结点的右孩子，也就是x的叔叔节点不为空，且为红色
  22.             if ((xppr = xpp.right) != null && xppr.red) {
  23.                 // 父节点和叔叔节点都为红色，只需要变色，且将x替换为祖父节点然后进行递归
  24.                 xppr.red = false;
  25.                 xp.red = false;
  26.                 xpp.red = true;
  27.                 x = xpp;
  28.             }
  29.             // 如果叔叔节点为空，或者为黑色
  30.             else {
  31.                 // 如果x节点为xp的右孩子
  32.                 if (x == xp.right) {
  33.                     // 先进行左旋，并且把x替换为xp进行递归，在左旋的过程中产生了新的root节点
  34.                     root = rotateLeft(root, x = xp);
  35.                     // x替换后，修改xp和xpp
  36.                     xpp = (xp = x.parent) == null ? null : xp.parent;
  37.                 }
  38.                 // 如果x本来是左孩子，或者已经经过了上面的左旋之后，进行变色加右旋
  39.                 if (xp != null) {
  40.                     xp.red = false;
  41.                     if (xpp != null) {
  42.                         xpp.red = true;
  43.                         root = rotateRight(root, xpp);
  44.                     }
  45.                 }
  46.             }
  47.         }
  48.         // 如果x的父节点是祖父结点的右孩子
  49.         else {
  50.             if (xppl != null && xppl.red) {
  51.                 xppl.red = false;
  52.                 xp.red = false;
  53.                 xpp.red = true;
  54.                 x = xpp;
  55.             }
  56.             else {
  57.                 if (x == xp.left) {
  58.                     root = rotateRight(root, x = xp);
  59.                     xpp = (xp = x.parent) == null ? null : xp.parent;
  60.                 }
  61.                 if (xp != null) {
  62.                     xp.red = false;
  63.                     if (xpp != null) {
  64.                         xpp.red = true;
  65.                         root = rotateLeft(root, xpp);
  66.                     }
  67.                 }
  68.             }
  69.         }
  70.     }
  71. }

HashMap中红黑树的左右旋操作

  1. static <K,V> TreeNode<K,V> rotateLeft(TreeNode<K,V> root,
  2.                                       TreeNode<K,V> p) {
  3.     // pp是祖父结点
  4.     // p是待旋转结点
  5.     // r是p的右孩子结点
  6.     // rl是r的左孩子结点
  7.     TreeNode<K,V> r, pp, rl;
  8.     if (p != null && (r = p.right) != null) {
  9.         // 如果rl不为空，则设置p.right=rl
  10.         if ((rl = p.right = r.left) != null)
  11.             rl.parent = p;
  12.         // 如果祖父结点为null，那么r设置为黑色，r左旋之后即为root节点
  13.         if ((pp = r.parent = p.parent) == null)
  14.             (root = r).red = false;
  15.         // 如果待旋转结点是左孩子节点
  16.         else if (pp.left == p)
  17.             pp.left = r;
  18.         // 如果待旋转结点为右孩子
  19.         else
  20.             pp.right = r;
  21.         r.left = p;
  22.         p.parent = r;
  23.     }
  24.     return root;
  25. }
  27. static <K,V> TreeNode<K,V> rotateRight(TreeNode<K,V> root,
  28.                                        TreeNode<K,V> p) {
  29.     TreeNode<K,V> l, pp, lr;
  30.     if (p != null && (l = p.left) != null) {
  31.         if ((lr = p.left = l.right) != null)
  32.             lr.parent = p;
  33.         if ((pp = l.parent = p.parent) == null)
  34.             (root = l).red = false;
  35.         else if (pp.right == p)
  36.             pp.right = l;
  37.         else
  38.             pp.left = l;
  39.         l.right = p;
  40.         p.parent = l;
  41.     }
  42.     return root;
  43. }

HashMap中的树化

  1. final void treeify(Node<K,V>[] tab) {
  2.     TreeNode<K,V> root = null;
  3.     // 遍历当前链表
  4.     for (TreeNode<K,V> x = this, next; x != null; x = next) {
  5.         next = (TreeNode<K,V>)x.next;
  6.         x.left = x.right = null;
  7.         if (root == null) {
  8.             x.parent = null;
  9.             x.red = false;
  10.             root = x;
  11.         }
  12.         else {
  13.             K k = x.key;
  14.             int h = x.hash;
  15.             Class<?> kc = null;
  16.             // 每遍历一个链表上的元素就插入到红黑树中
  17.             for (TreeNode<K,V> p = root;;) {
  18.                 int dir, ph;
  19.                 K pk = p.key;
  21.                 // 判断待插入结点应该插入在左子树还是右子树
  22.                 // 先比较hash值
  23.                 if ((ph = p.hash) > h)
  24.                     dir = -1;
  25.                 else if (ph < h)
  26.                     dir = 1;
  27.                 // 如果hash值相等，然后比较k.compareTo(pk)
  28.                 else if ((kc == null &&
  29.                           (kc = comparableClassFor(k)) == null) ||
  30.                          (dir = compareComparables(kc, k, pk)) == 0)
  31.                     // 如果还相等则再比较identityHashCode
  32.                     dir = tieBreakOrder(k, pk);
  34.                 // 根据dir的值就知道了待插入结点该插在左子树还是右子树了
  35.                 TreeNode<K,V> xp = p;
  36.                 if ((p = (dir <= 0) ? p.left : p.right) == null) {
  37.                     x.parent = xp;
  38.                     if (dir <= 0)
  39.                         xp.left = x;
  40.                     else
  41.                         xp.right = x;
  42.                     root = balanceInsertion(root, x);
  43.                     break;
  44.                 }
  45.             }
  46.         }
  47.     }
  48.     moveRootToFront(tab, root);
  49. }