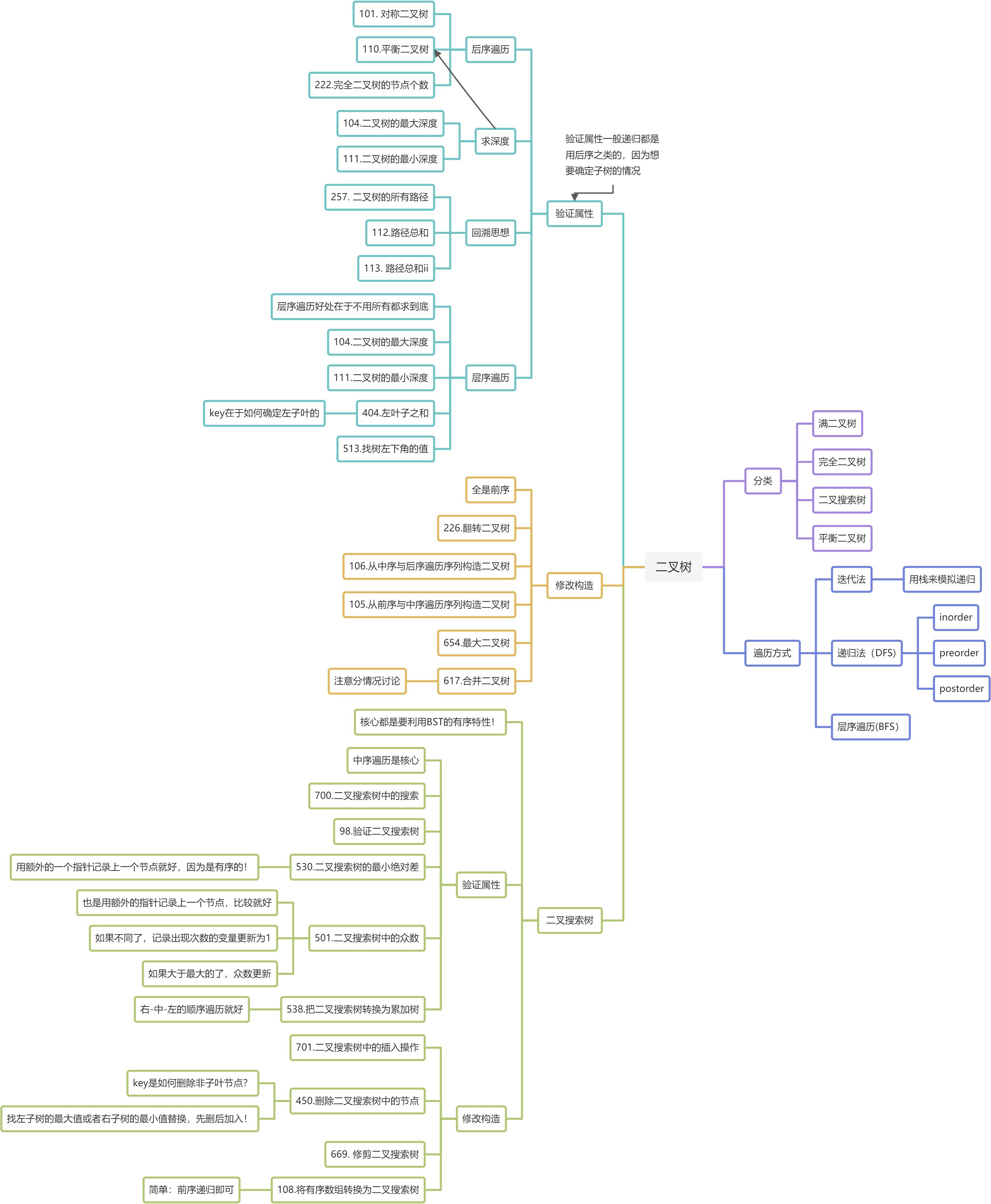
二叉树 - 图1

二叉树的遍历

:::info 二叉树的遍历分为：

  • 前序：root-leftTree-rightTree
  • 中序：leftTree-root-rightTree

  • 后续：leftTree-rightTree-root ::: 这些顺序的分别在于何时处理当前节点；在dfs遍历的过程中，一个节点会被经过3次；

    1. void traverse(TreeNode* root){
    2.   //first time---preorder
    3.   traverse(root->left);
    4.   //second time---inorder
    5.   traverse(root->right);
    6.   //third time---postorder
    7. }

    :::tips 三种遍历各有特点:

  • 前序：不需要知道子树的内容

  • 中序：已经知道左子树的内容
  • 后序：知道了两个子树的内容

如果要知道子树的内容，一般是后续 :::

递归的题

:::info 二叉树有两种题：一种要递归遍历，一种要分情况讨论；
递归的题如果需要知道下面子树的情况，大多是后序遍历！ :::

递归改迭代

递归改迭实际上不会减少多少空间复杂度，只是自己操作栈或队列来替代了系统压栈

  1. stack<TreeNode*> st;
  2. if(root==nullptr)
  3.     return;
  4. st.push(st);
  5. while(!st.empty()){
  6.     TreeNode* cur=st.top();
  7.     st.pop();
  8.     if(cur->right!=nullptr) st.push(cur->right);
  9.     //先入后出
  10.     if(cur->left!=nullptr) st.push(cur->left);
  11.     //处理cur节点
  12. }

:::info 前序用的是stack :::

  1. stack<TreeNode*> st;
  2. if(root==nullptr)
  3.     return;
  4. st.push(st);
  5. while(!st.empty()){
  6.     TreeNode* cur=st.top();
  7.     st.pop();
  8.     if(cur->left!=nullptr) st.push(cur->right);
  9.     //先入后出
  10.     if(cur->right!=nullptr) st.push(cur->right);
  11.     //处理cur节点
  12.     vec.push_back(cur->val);
  13. }
  14. reverse(vec.begin(),vec.end));

:::danger 只能是用数组存了后reverse；如果不是遍历而是做其他操作，那么需要递归吧 :::

  1. class Solution {
  2. public:
  3.     vector<int> inorderTraversal(TreeNode* root) {
  4.         vector<int> result;
  5.         stack<TreeNode*> st;
  6.         TreeNode* cur = root;
  7.         while (cur != NULL || !st.empty()) {
  8.             if (cur != NULL) { // 指针来访问节点，访问到最底层
  9.                 st.push(cur); // 将访问的节点放进栈
  10.                 cur = cur->left;                // 左
  11.             } else {
  12.                 cur = st.top(); 
  13.                 // 从栈里弹出的数据，就是要处理的数据（放进result数组里的数据）
  14.                 st.pop();
  15.                 result.push_back(cur->val);     // 中
  16.                 cur = cur->right;               // 右
  17.             }
  18.         }
  19.         return result;
  20.     }
  21. };

:::tips 中序和前序后续都不一样！ :::

层序遍历（BFS)

:::info 层序遍历的核心是会用到额外的容器去存下下一层需要遍历的节点；

  • 二叉树里有，图中也有、二维数组里也可以有

  • 二叉树中用queue：队列，先入先出。 :::

    1. //input TreeNode* root
    2. if(root==nullptr)
    3.   return {};
    4. queue<TreeNode*> que;
    5. vector<int> vec;
    6. que.push(root);
    7. while(!que.empty()){
    8.   int sz=que.size();//先要去确定当前一层有多少节点
    9.   for(int i=0;i<sz;i++){
    10.       TreeNode*cur=que.front();
    11.       que.pop();
    12.       if(cur->left!=nullptr) que.push(cur->left);
    13.       if(cur->right!=nullptr) que.push(cur->right);
    14.       vec.push_back(cur->val);
    15.       //处理当前节点
    16.   }
    17. }

    :::info 层序遍历需要注意的点：

  • 循环中不能用que.size()因为在每轮迭代中都会插入节点，会变，需要在每一层开始前求出size

  • 可以改变的地方有插入节点的顺序：先左后右还是先右后左 :::

    二叉树中的回溯

    何时需要返回值？

  • 如果需要搜索整棵二叉树且不用处理递归返回值，递归函数就不要返回值。（这种情况就是本文下半部分介绍的113.路径总和ii）

  • 如果需要搜索整棵二叉树且需要处理递归返回值，递归函数就需要返回值。 （这种情况我们在236. 二叉树的最近公共祖先(opens new window)中介绍）
  • 如果要搜索其中一条符合条件的路径，那么递归一定需要返回值，因为遇到符合条件的路径了就要及时返回。（本题的情况）