一个简单的能够完成手写数字分类的网络

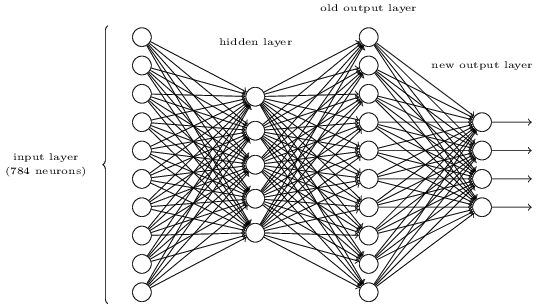
一个简单的能够完成手写数字分类的网络

定义了神经网络，我们回头看下手写数字的识别问题。这个问题可以切分为两个子问题，首先，把包含有多个手写数字的图片分割为一系列的图片，每个图片只包含单个手写数字。如下：

拆开为6个单的手写字

人类轻松可以完成这个分段问题，但对于计算机来说仍然具有一定的挑战性。完成了图片的划分，第二问题是，程序需要将每张图片按照其上面的数字进行分类。例如，如果我们想让程序识别出第一个图片，数字5.

我们将聚焦在通过程序解决第二个问题。原因是，当你找到对单个数字进行分类的方法后，会发现对图片进行分段的问题并不是那么难了。其中一个可能的方法是，可以测试很多不同的图片分段方法，然后使用单个数字分类法来对每个分段方法打分。如果单个数字分类法在对所有分段进行分类时都很有信心，这分段方法就可以获得高分。相反，如果在对一个或多个分段进行分类时遇到了麻烦，就得低分，因为造成分类困难的原因很可能是我们分段选择错了。这个方法及其其它的变种可以很好地解决图片分段问题。所以，我们将聚焦于开发出一个神经网络来，以解决更加有趣和更难的问题上，名义上，识别单个手写数字。

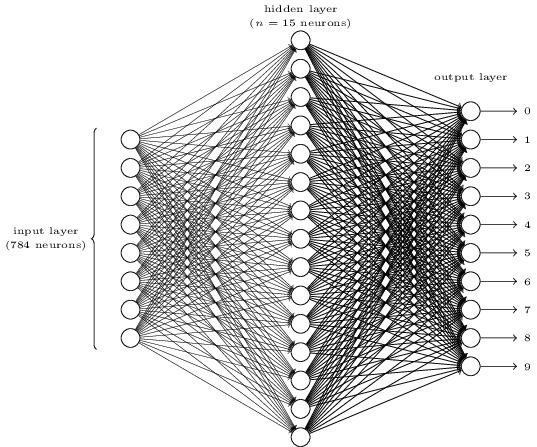
输入层包含了由输入像素神经元编码而来的神经元，如前所述，网络的训练数据包含了许多28 x 28像素的手写数字扫描数据，所以，输入层包含了28 x 28=784个神经元。简化期间，我在上图中忽略了大部分神经元。输入像素为灰度，0.0代表白色，1.0代表黑色，之间的数值代表灰色的等级。

第二层是隐藏层。我们把每个隐藏层神经元数量指定为n，后续我们将测试几个不同的n的数值。上面的例子描述的是一个小的隐藏层，它包含了15个神经元。

输出层包括了10个神经元。如果第一个神经元发射了，比如输出约等于1，那么就表示网络认为数字为0.如果第二个神经元发射了就意味着网络认为数字为1.以此类推。为了精确期间，我们会对输出神经元从0到9进行编号，如何看那个神经元有最大的激活数值。如果这个神经元的编号是6，那么网络的猜测结果就是6.其它的输出神经元类似。

你可能在想，为什么用10个输出神经元。毕竟，结果是要告诉我们0-9中那个对应于输入的图片。一个看起来自然的方法是仅使用四个输出神经元，每个神经元都当做一个比特的数值，这样组成了一个四位的二进制数。然后看每个神经元接近于0还是1，这样同样可以给出网络预测的结果。为什么要用10个输出神经元呢？会不会低效？最终的判定是通过实验完成的。这两种方法我们都可以去尝试，最终的结果是，对于这个问题而言，10个输出神经元要比4个神经元能够更好地学习识别数字。留给我们的问题是，为什么10个神经元会好一些。是否有一个启发式可以事前告诉我们我们应该用10个神经元而不是4个神经元。

为了弄明白为什么这么做，这能帮助我们思考从第一条定律开始，神经元是如何工作的。考虑第一种使用10个神经元的情况。我们先聚焦于第一个输出神经元，它试图决定数字是否0。它通过从隐藏层中权衡每个输入来完成判断。这些隐藏层是做什么的？为方便讨论起见，假如隐藏层的第一个神经元探测是否存在下面的图片：

如果输入的像素与这张图片重叠的像素，就输入的像素赋予较重的权重，对其他输入赋予较低的权重。类似地，隐藏层的第二、第三和第四个神经元来决定下述图片是否存在。

你可能已经猜到了，这四张图片组成了数字0.

如果这四个隐藏的神经元都发射了，我们就可以认为数字是0. 当然，这不是唯一的得出数字为0结论的方法。实际上我们可以有需要其他的方法。但看起来在这种情况下，我们可以有信心地说我们认为输入的数字是0.

假如神经网络是这么工作的，我们就可以给出比较有说服力的解释，为什么10个输出要优于4个输出。如果我们有4个输出，第一个输出神经元需要通过输入的数字来决定最显著的比特是什么。但是，把上述简单的图形与最显著的比特关联起来，貌似没有特别容易的办法。很难想象一个数字的一部分是如何和最显著的输出比特关联起来的。

现在，如前所述，这仅仅是基于现有经验得出的。刚才的例子中，隐藏层用来探测简单的图形形状，但这并不是说这个三层神经网络必须像我描述的这样工作。或许一个聪明的学习算法可以得出一种权重组合，这样我们就可以仅仅使用4个输出神经元。不过，基于启发式的思考方法，我已经能够很好地描述它的工作机制了，还能在设计好的神经网络时帮你节省很多时间。

练习

还是有办法通过二级制的方法表达一个数字的，只要在第三层的基础上增加一层就可以了。新增加的层把前一层的输出转化为二级制表达，如下图所示。假设第三层中数字正确的神经元输出值至少为0.99，否则最大为0.01. 请试着找到合适的权重和偏移量。