关于狄克斯特拉算法，我主要是在《算法图解》一书中发现解释的并不清楚，所以找了博客学习，Google以后发现这篇英文博客讲解的不错，并且给出了C++，Java和C#下的代码实现。我将自己的理解用PPT做了下来，将图片放入，后文给出代码实现。

一、例子

图1. 问题

图2. 第一步+第二步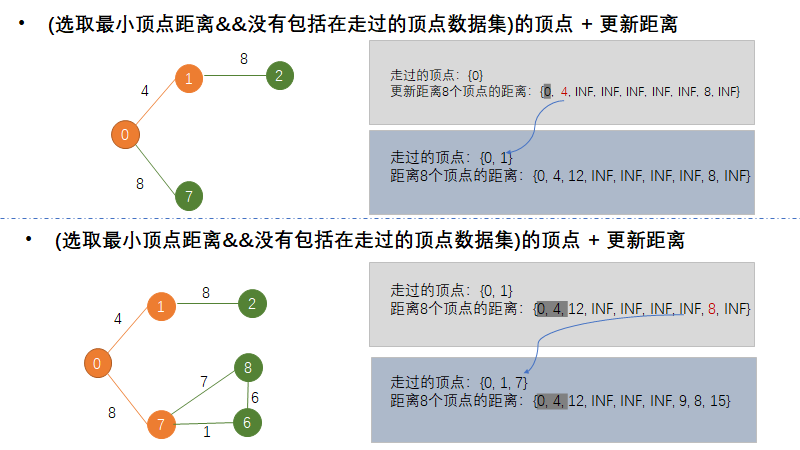

图3. 第三步+第四步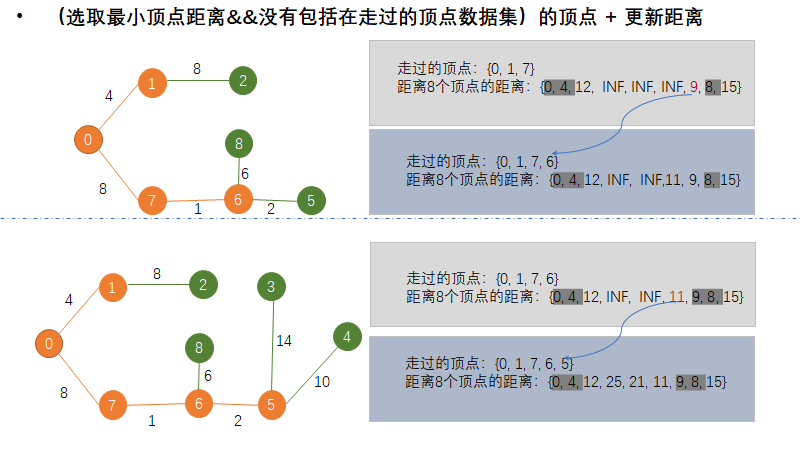

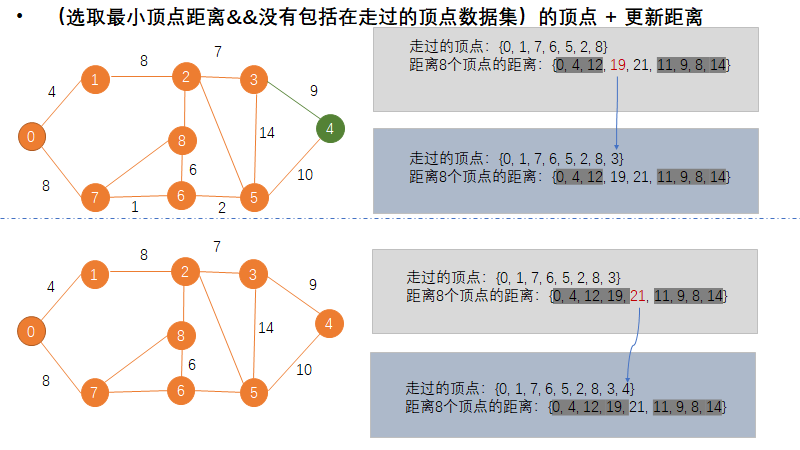
图4. 第五步+第六步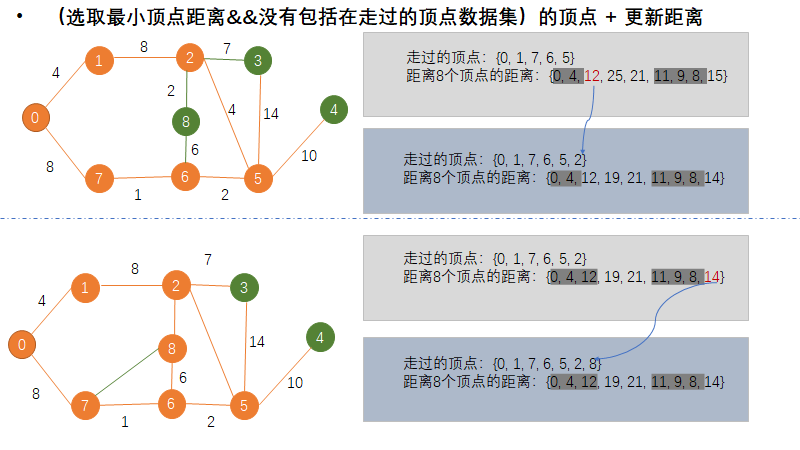

图5. 第七步+第八步

更新距离的方法： 例如上面现在更新到了顶点2，且顶点2对应的距离为中的12；且走过的邻点所以只需要更新3和8的邻点距离。

即与邻点8的距离更新为：； 与邻点3的邻点距离更新为

图6. 第九步+第十步

二、代码实现

// A C++ program for Dijkstra's single source shortest path algorithm.
// The program is for adjacency matrix representation of the graph.
#include <limits.h>
#include <stdio.h>
// Number of vertices in the graph
#define vertex 9
// A utility function to find the vertex with minimum distance value, from 
// the set of vertices not yet included in shortest path tree.
int minDistance(int dist[], bool sptSet[])
{
    //Initialize min value
    int min = INT_MAX, minIndex;
    for (int v = 0; v < vertex; v++)
    {
        if (sptSet[v] == false && dist[v] <= min)
        {
            min = dist[v], minIndex = v;
        }
    }
    return minIndex;
}
// A utility function to print the constructed distance array
void printSolution(int dist[])
{
    printf("Vertex \t\t Distance from Source\n");
    for (int i = 0; i < vertex; i++)
    {
        printf("%d \t\t %d\n", i, dist[i]);
    }
}
// Function that implements Dijkstra's single source shortest path algorithm
// for a graph represented using adjacency matrix representation.
void dijkstra(int graph[vertex][vertex], int src)
{
    int dist[vertex];            // The output array. dist[i] will hold the shortest distance from src to i
    bool sptSet[vertex];        // sptSet[i] will be true if vertex i is included in shortest path tree or shortest
    //distance from src to i is finalized.
    // Initialize all distance as INFINITE and sptSet[] as false.
    for (int i = 0; i < vertex; i++)
    {
        dist[i] = INT_MAX, sptSet[i] = false;
    }
    // Distance of source vertex from itself is always 0
    dist[src] = 0;
    // Find shortest path for all vertices
    for (int count = 0; count < vertex - 1; count++)
    {
        // Pick the minimum distance vertex from the set of vertices not yet processed. u is always equal to 
        // src in the first iteration.
        int u = minDistance(dist, sptSet);
        // Mark the picked vertex as processed
        sptSet[u] = true;
        // Update dist value of the adjacent vertices of the picked vertex
        for (int v = 0; v < vertex; v++)
        {
            // Update dist[v] only if is not in sptSet, there is an edge fron u to v, and total weight of path
            // from src to v through u is smaller than current value of dist[v]
            if (!sptSet[v] && graph[u][v] && dist[u] != INT_MAX && dist[u] + graph[u][v] < dist[v])
            {
                dist[v] = dist[u] + graph[u][v];
            }
        }
    }
    // print the constructed distance array
    printSolution(dist);
}
// driver program to test above function 
int main()
{
    /* Let us create the example graph discussed above */
    int graph[vertex][vertex] = { { 0, 4, 0, 0, 0, 0, 0, 8, 0 },
                        { 4, 0, 8, 0, 0, 0, 0, 11, 0 },
                        { 0, 8, 0, 7, 0, 4, 0, 0, 2 },
                        { 0, 0, 7, 0, 9, 14, 0, 0, 0 },
                        { 0, 0, 0, 9, 0, 10, 0, 0, 0 },
                        { 0, 0, 4, 14, 10, 0, 2, 0, 0 },
                        { 0, 0, 0, 0, 0, 2, 0, 1, 6 },
                        { 8, 11, 0, 0, 0, 0, 1, 0, 7 },
                        { 0, 0, 2, 0, 0, 0, 6, 7, 0 } };
    dijkstra(graph, 0);
    return 0;
}

Vertex Distance from Source 0 0

1 4

2 12

3 19

4 21

5 11

6 9

7 8

8 14

可以看到和我们上面得到的结果一致。