排序算法：插入、冒泡、选择、希尔、快速、归并、堆排序、计数排序、桶排序、基数排序
查找算法：线性查找、二分查找
线性数据结构：动态数组、链表、栈、队列、哈希表
经典树结构：二分搜索树、堆、AVL、红黑树、B类树
高级数据结构：线段树、并查集、Trie、SQRT分解
字符串算法：KMP、模式匹配

什么是算法：一系列解决问题的、清晰的、可执行的计算机指令

  • 有限性
  • 确定性：不会产生二义性
  • 可行性
  • 输入
  • 输出

查找算法

线性查找

简单示例，在数组中查找某个数

  1. public static int search(int[] data, int target){
  2.     for (int i=0; i<data.length; i++) {
  3.         if (data[i] == target){
  4.             return i;
  5.         }
  6.     }
  7.     return -1;
  8. }
  1. 再改进，使用标准的泛型。这里注意细节，使用泛型后比较要调用  `.equals()`方法
  1. public static <E> int search(E[] data, E target){
  2.     for (int i=0; i<data.length; i++) {
  3.         if (data[i].equals(target)){
  4.             return i;
  5.         }
  6.     }
  7.     return -1;
  8. }

二分查找

二分查找法只针对有序数列，其时间复杂度为算法与数据结构 - 图1

  1. public class BinarySearch {
  2.     private BinarySearch(){}
  4.     public static <E extends Comparable<E>> int search(E[] arr, E target){
  5.         return search(arr, 0, arr.length-1, target);
  6.     }
  8.     public static <E extends Comparable<E>> int search(E[] arr, int l, int r, E target){
  9.         int half = l + (r-l)/2;
  10.         if (l>r){
  11.             return -1;
  12.         }
  13.         if (arr[half].compareTo(target) == 0){
  14.             return half;
  15.         }
  16.         if (arr[half].compareTo(target) > 0){
  17.             return search(arr, l, half-1, target);
  18.         }
  19.         return search(arr, half+1, r, target);
  20.     }
  21. }

二分搜索树

二分搜索树（Binary Search Tree）首先是二叉树，二分搜索树每个节点的值大于其左子树所有节点的值小于其右子树的所有节点的值，存储的元素必须具有可比较性

排序算法

排序算法是为了让数据有序，排序算法中蕴含着重要的算法设计思想。

选择排序

先把最小的拿出来，剩下的再把最小的拿出来，以此往复，直至没有剩下的。
上述的说法在排序过程中占用了额外的空间，考虑进行原地排序，即不开辟额外的数组空间。
下面示例直接加上泛型，一步到位

  1. public class SelectSort {
  3.     private SelectSort() {
  4.     }
  6.     public static <E extends Comparable<E>> E[] sort(E[] data) {
  7.         for (int i = 0; i < data.length; i++) {
  8.             int tempIndex = i;
  9.             for (int j = i + 1; j < data.length; j++) {
  10.                 if (data[j].compareTo(data[tempIndex]) < 0) {
  11.                     tempIndex = j;
  12.                 }
  13.             }
  14.             E temp = data[tempIndex];
  15.             data[tempIndex] = data[i];
  16.             data[i] = temp;
  17.         }
  18.         return data;
  19.     }
  21.     public static void main(String[] args) {
  22.         Integer[] data = {12, 3, 6, 2, 3, 7, 53, 24};
  23.         Integer[] sort = SelectSort.sort(data);
  24.         for (int value : sort) {
  25.             System.out.println(value);
  26.         }
  27.     }
  28. }
  1. 比较一个自定义类
  1. public class Student implements Comparable<Student > {
  3.     private String name;
  4.     private Integer score;
  6.     public Student(String name, Integer score){
  7.         this.name = name;
  8.         this.score = score;
  9.     }
  11.     public String getName() {
  12.         return name;
  13.     }
  15.     public void setName(String name) {
  16.         this.name = name;
  17.     }
  19.     public Integer getScore() {
  20.         return score;
  21.     }
  23.     public void setScore(Integer score) {
  24.         this.score = score;
  25.     }
  27.     @Override
  28.     public int compareTo(Student stu) {
  29.         return this.score.compareTo(stu.score);
  30.     }
  32.     @Override
  33.     public int hashCode() {
  34.         int result = 17;
  35.         result = 31*result + (name == null ? 0 : name.hashCode());
  36.         result = 31*result + (score == null ? 0 : score.hashCode());
  37.         return result;
  38.     }
  40.     @Override
  41.     public boolean equals(Object obj) {
  42.         if (obj == null){
  43.             return false;
  44.         }
  45.         if (obj.getClass() != Student.class){
  46.             return false;
  47.         }
  48.         Student student = (Student) obj;
  49.         return this.name.equals(student.name);
  50.     }
  52.     @Override
  53.     public String toString() {
  54.         return this.name+":"+this.score;
  55.     }
  56. }
  1. public static void main(String[] args) {
  2.     //Integer[] data = {12, 3, 6, 2, 3, 7, 53, 24};
  3.     //Integer[] sort = SelectSort.sort(data);
  4.     //for (int value : sort) {
  5.     //    System.out.println(value);
  6.     //}
  7.     Student[] students = {new Student("Jack",12),
  8.                           new Student("Bob",23),
  9.                           new Student("DuoBi",18),
  10.                           new Student("Nancy",3),
  11.                           new Student("Rose",9)};
  12.     Student[] sortStu = SelectSort.sort(students);
  13.     for (Student stu : sortStu) {
  14.         System.out.println(stu.toString());
  15.     }
  16. }
  1. 选择排序的时间复杂度是![](https://cdn.nlark.com/yuque/__latex/51674eb85c98a46ed4b404e6e160bce5.svg#card=math&code=%20o%20%20%28n%5E%7B2%7D%20%29&id=O8ZQl)

插入排序

实现示例

  1. public static <E extends Comparable<E>> E[] sort(E[] data) {
  2.     int length = data.length;
  3.     for (int i = 0; i < length; i++) {
  4.         for (int j = i; j > 1; j--) {
  5.             if (data[j].compareTo(data[j - 1])<0) {
  6.                 E temp = data[j];
  7.                 data[j] = data[j - 1];
  8.                 data[j - 1] = temp;
  9.             }
  10.         }
  11.     }
  12.     return data;
  13. }
  1. 时间复杂度是![](https://cdn.nlark.com/yuque/__latex/51674eb85c98a46ed4b404e6e160bce5.svg#card=math&code=%20o%20%20%28n%5E%7B2%7D%20%29&id=h4ZnM)<br />上述的例子可以再优化一下，减少一下时间
  1. public static <E extends Comparable<E>> E[] sort(E[] data) {
  2.     int length = data.length;
  3.     for (int i = 0; i < length; i++) {
  4.         E temp = data[i];
  5.         int j;
  6.         for (j = i; j >= 1 && temp.compareTo(data[j - 1])<0; j--) {
  7.             data[j] = data[j - 1];
  8.         }
  9.         data[j] = temp;
  10.     }
  11.     return data;
  12. }
  1. 对于插入排序，如果目标数组已经有序了，则时间复杂度只有![](https://cdn.nlark.com/yuque/__latex/5889c147a0f3935f2ce6e6e74c73a974.svg#card=math&code=%20o%20%20%28n%20%29&id=b9VHf)；相比于选择排序，选择排序的复杂度永远是![](https://cdn.nlark.com/yuque/__latex/51674eb85c98a46ed4b404e6e160bce5.svg#card=math&code=%20o%20%20%28n%5E%7B2%7D%20%29&id=AjmHu)

归并排序

是复杂的递归算法，时间复杂度为算法与数据结构 - 图2
将数组化为两个子数组，对每个子数组进行排序，子数组再化为子数组排序，以此类推…
image.png
重点在于归并的过程，即merge(arr, l, mid, r)，归并的过程无法原地进行

  1. public static <E extends Comparable<E>> void sort(E[] arr) {
  2.     sort(arr, 0, arr.length - 1);
  3. }
  5. private static <E extends Comparable<E>> void sort(E[] arr, int l, int r) {
  6.     if (l >= r) {
  7.         return;
  8.     }
  9.     int mid = l + (r - l) / 2;
  10.     sort(arr, l, mid);
  11.     sort(arr, mid + 1, r);
  12.     merge(arr, l, mid, r);
  13. }
  15. /**
  16.  * 合并两个有序区间 arr[l,mid]和 arr[mid+1,l]
  17. */
  18. private static <E extends Comparable<E>> void merge(E[] arr, int l, int mid, int r) {
  19.     E[] temp = Arrays.copyOfRange(arr, l, r + 1);
  20.     int i = l;
  21.     int j = mid + 1;
  22.     for (int k = l; k <= r; k++) {
  23.         if (i > mid) {
  24.             arr[k] = temp[j - l];
  25.             j++;
  26.         } else if (j > r) {
  27.             arr[k] = temp[i - l];
  28.             i++;
  29.         } else if (temp[i-l].compareTo(temp[j-l]) >= 0) {
  30.             arr[k] = temp[j - l];
  31.             j++;
  32.         } else {
  33.             arr[k] = temp[i - l];
  34.             i++;
  35.         }
  36.     }
  37. }
  1. 对于复杂度的分析<br />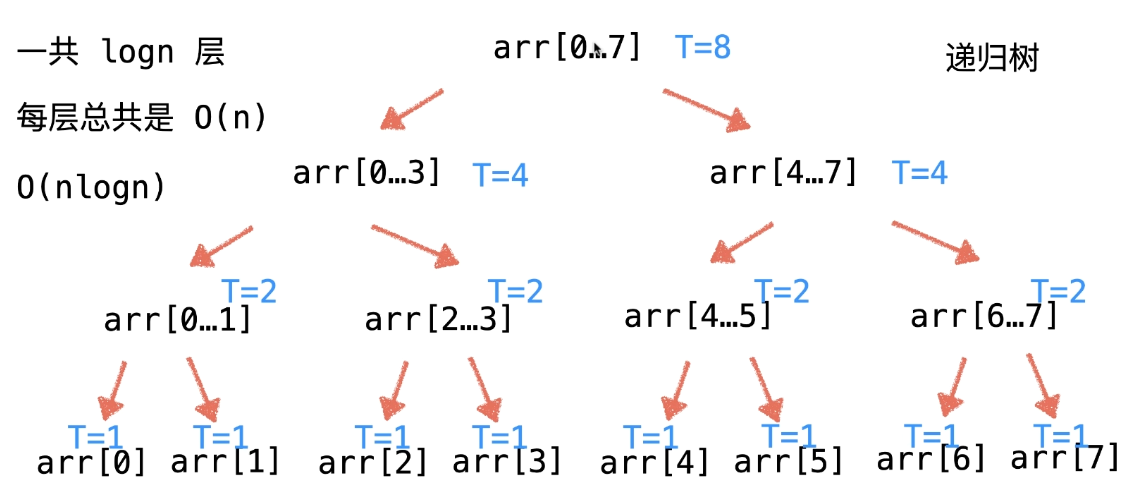![image.png](https://cdn.nlark.com/yuque/0/2021/png/2961643/1640766394116-e5336f97-67ed-4eff-b346-879a73989962.png#clientId=uac58de8b-3400-4&from=paste&height=496&id=ua9ffada4&margin=%5Bobject%20Object%5D&name=image.png&originHeight=496&originWidth=1136&originalType=binary&ratio=1&size=134606&status=done&style=none&taskId=ud2316521-8deb-4a23-983e-e6018e201a8&width=1136)

对上述代码的优化

  1. public static <E extends Comparable<E>> void sort(E[] arr) {
  2.     E[] temp = Arrays.copyOf(arr, arr.length);
  3.     sort(arr, 0, arr.length - 1, temp);
  4. }
  6. private static <E extends Comparable<E>> void sort(E[] arr, int l, int r, E[] temp) {
  7.     if (l >= r) {
  8.         return;
  9.     }
  10.     int mid = l + (r - l) / 2;
  11.     sort(arr, l, mid, temp);
  12.     sort(arr, mid + 1, r, temp);
  13.     if (arr[mid].compareTo(arr[mid+1])>0){
  14.         merge(arr, l, mid, r, temp);
  15.     }
  17. }
  19. /**
  20.  * 合并两个有序区间 arr[l,mid]和 arr[mid+1,l]
  21. */
  22. private static <E extends Comparable<E>> void merge(E[] arr, int l, int mid, int r, E[] temp) {
  23.     System.arraycopy(arr, l, temp, 0, r-l+1);
  24.     int i = l;
  25.     int j = mid + 1;
  26.     for (int k = l; k <= r; k++) {
  27.         if (i > mid) {
  28.             arr[k] = temp[j - l];
  29.             j++;
  30.         } else if (j > r) {
  31.             arr[k] = temp[i - l];
  32.             i++;
  33.         } else if (temp[i-l].compareTo(temp[j-l]) >= 0) {
  34.             arr[k] = temp[j - l];
  35.             j++;
  36.         } else {
  37.             arr[k] = temp[i - l];
  38.             i++;
  39.         }
  40.     }
  41. }
  1. 此时，对归并的时候进行了优化。优化后，如果数组是有序的，则排序的时间复杂度为![](https://cdn.nlark.com/yuque/__latex/5889c147a0f3935f2ce6e6e74c73a974.svg#card=math&code=%20o%20%20%28n%20%29&id=pnnlc)；并且不用每次归并之时都创建一个新的数组，节省了空间

此外，上述可以看出是自顶向下的归并，我们还可以用自底向上的归并

  1. /**
  2.  * 自底向上的归并
  3. */
  4. public static <E extends Comparable<E>> void sortBU(E[] arr) {
  5.     int n = arr.length;
  6.     E[] temp = Arrays.copyOf(arr, n);
  7.     for (int sz = 1; sz < n; sz += sz) {
  8.         for (int i = 0; i + sz < n; i += sz + sz) {
  9.             if (arr[i + sz - 1].compareTo(arr[i + sz])>0){
  10.                 merge(arr, i, i + sz - 1, Math.min(i + 2 * sz - 1, n - 1), temp);
  11.             }
  12.         }
  13.     }
  14. }
  16. /**
  17.  * 合并两个有序区间 arr[l,mid]和 arr[mid+1,l]
  18. */
  19. private static <E extends Comparable<E>> void merge(E[] arr, int l, int mid, int r, E[] temp) {
  20.     System.arraycopy(arr, l, temp, 0, r - l + 1);
  21.     int i = l;
  22.     int j = mid + 1;
  23.     for (int k = l; k <= r; k++) {
  24.         if (i > mid) {
  25.             arr[k] = temp[j - l];
  26.             j++;
  27.         } else if (j > r) {
  28.             arr[k] = temp[i - l];
  29.             i++;
  30.         } else if (temp[i-l].compareTo(temp[j-l]) >= 0) {
  31.             arr[k] = temp[j - l];
  32.             j++;
  33.         } else {
  34.             arr[k] = temp[i - l];
  35.             i++;
  36.         }
  37.     }
  38. }

快速排序

快速排序就和它的名字一样很快，它的核心是选取一个数然后使得左边的数都比它小右边的数都比它大，然后对左右重复这个操作

  1. public static <E extends Comparable<E>> void sort(E[] arr) {
  2.     sort(arr, 0, arr.length - 1);
  3. }
  5. private static <E extends Comparable<E>> void sort(E[] arr, int l, int r) {
  6.     if (l >= r) {
  7.         return;
  8.     }
  9.     int partition = partition(arr, l, r);
  10.     sort(arr, l, partition);
  11.     sort(arr, partition + 1, r);
  12. }
  14. private static <E extends Comparable<E>> int partition(E[] arr, int l, int r) {
  15.     int j = l;
  16.     for (int i = l + 1; i <= r; i++) {
  17.         if (arr[i].compareTo(arr[l]) < 0) {
  18.             j++;
  19.             swap(arr, i, j);
  20.         }
  21.     }
  22.     swap(arr, l, j);
  23.     return j;
  24. }
  26. private static <E extends Comparable<E>> void swap(E[] arr, int i, int j) {
  27.     E temp = arr[i];
  28.     arr[i] = arr[j];
  29.     arr[j] = temp;
  30. }
  1. 这种写法有一个问题，当数组本身就是有序的时，该算法的时间复杂度是![](https://cdn.nlark.com/yuque/__latex/51674eb85c98a46ed4b404e6e160bce5.svg#card=math&code=%20o%20%20%28n%5E%7B2%7D%20%29&id=iEvA5)，会非常慢；而且递归深度是![](https://cdn.nlark.com/yuque/__latex/e31f1d7b55ede020a79e96e64abdaa0d.svg#card=math&code=%20o%20%20%28n%29&id=Hd2fM)，容易造成栈溢出<br />可以从数组中随机一个数出来，把随机数和第一个数交换（即随机数为第一个元素），其他操作都不变
  1. public class QuickSort {
  2.     private QuickSort() {
  3.     }
  5.     private static Random random = new Random();
  7.     public static <E extends Comparable<E>> void sort(E[] arr) {
  8.         sort(arr, 0, arr.length - 1);
  9.     }
  11.     private static <E extends Comparable<E>> void sort(E[] arr, int l, int r) {
  12.         if (l >= r) {
  13.             return;
  14.         }
  15.         int partition = partition(arr, l, r);
  16.         sort(arr, l, partition);
  17.         sort(arr, partition + 1, r);
  18.     }
  20.     private static <E extends Comparable<E>> int partition(E[] arr, int l, int r) {
  21.         //生成一个[l,r]间的随机索引
  22.         int randomIndex = random.nextInt(r - l + 1) + l;
  23.         swap(arr, l, randomIndex);
  24.         int j = l;
  25.         for (int i = l + 1; i <= r; i++) {
  26.             if (arr[i].compareTo(arr[l]) < 0) {
  27.                 j++;
  28.                 swap(arr, i, j);
  29.             }
  30.         }
  31.         swap(arr, l, j);
  32.         return j;
  33.     }
  35.     private static <E extends Comparable<E>> void swap(E[] arr, int i, int j) {
  36.         E temp = arr[i];
  37.         arr[i] = arr[j];
  38.         arr[j] = temp;
  39.     }
  40. }

对于上述的修改，虽然解决了数组本身就有序这种情况所造成的影响，但是如果数组所有的元素都一样时，排序的效率依然很低下。针对这个问题，引入双路快速排序算法
之前的做法，对于关键字v，我们把大于和小于v的都放在一边，下面我们考虑把大于和小于v的部分分别放在两边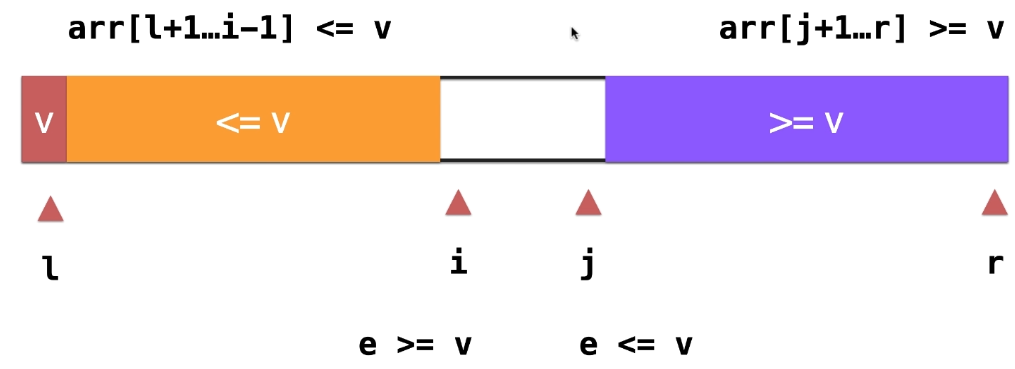
image.png
在代码层面，就是partition方法要做修改

  1. public class QuickSort {
  2.     private QuickSort() {
  3.     }
  5.     private static Random random = new Random();
  7.     public static <E extends Comparable<E>> void sort(E[] arr) {
  8.         sort(arr, 0, arr.length - 1);
  9.     }
  11.     private static <E extends Comparable<E>> void sort(E[] arr, int l, int r) {
  12.         if (l >= r) {
  13.             return;
  14.         }
  15.         int partition = partition(arr, l, r);
  16.         sort(arr, l, partition);
  17.         sort(arr, partition + 1, r);
  18.     }
  20.     private static <E extends Comparable<E>> int partition(E[] arr, int l, int r) {
  21.         //生成一个[l,r]间的随机索引
  22.         int randomIndex = random.nextInt(r - l + 1) + l;
  23.         swap(arr, l, randomIndex);
  25.         int i=l+1;
  26.         int j=r;
  27.         while (true) {
  28.             while (arr[i].compareTo(arr[l])<0 && i<=j){
  29.                 i++;
  30.             }
  31.             while (arr[j].compareTo(arr[l])>0 && i<=j){
  32.                 j--;
  33.             }
  34.             if (i>=j){
  35.                 break;
  36.             }
  37.             swap(arr, i, j);
  38.             i++;
  39.             j--;
  40.         }
  41.         swap(arr, l, j);
  42.         return j;
  43.     }
  45.     private static <E extends Comparable<E>> void swap(E[] arr, int i, int j) {
  46.         E temp = arr[i];
  47.         arr[i] = arr[j];
  48.         arr[j] = temp;
  49.     }
  50. }
  1. 上述代码中，虽然    `partition`方法中看似有两重循环，但是实际上数组每个元素只遍历了一遍，`partition`方法的复杂度只有![](https://cdn.nlark.com/yuque/__latex/e31f1d7b55ede020a79e96e64abdaa0d.svg#card=math&code=%20o%20%20%28n%29&id=yZAtD)<br />如果数组的元素全都重复的话，我们其实只用一次`partition`方法就行了，为此我们进一步优化，引入**三路快速排序算法**。即对于关键字v，大于v小于v和等于v的这三路<br />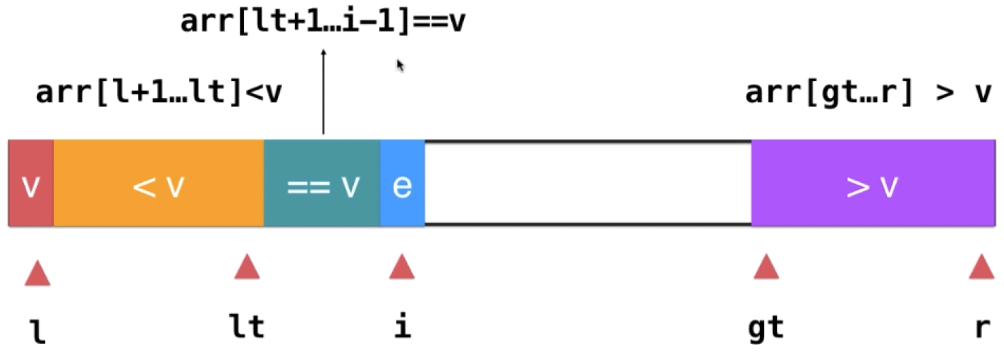![image.png](https://cdn.nlark.com/yuque/0/2022/png/2961643/1641352592625-aa38ec33-4eb9-40a3-9555-bec805ebb443.png#clientId=u666e96b3-c41a-4&from=paste&height=364&id=uc0a9614e&margin=%5Bobject%20Object%5D&name=image.png&originHeight=364&originWidth=1004&originalType=binary&ratio=1&size=60736&status=done&style=none&taskId=u56983b14-2cd0-451e-be76-09c30fb5039&width=1004)<br />对于三路快速排序算法，如果数组中所有的元素都相同，则时间复杂度为![](https://cdn.nlark.com/yuque/__latex/e31f1d7b55ede020a79e96e64abdaa0d.svg#card=math&code=%20o%20%20%28n%29&id=CIzPc)
  1. public class QuickSort {
  2.     private QuickSort() {
  3.     }
  5.     private static Random random = new Random();
  7.     public static <E extends Comparable<E>> void sort(E[] arr) {
  8.         sort(arr, 0, arr.length - 1);
  9.     }
  11.     private static <E extends Comparable<E>> void sort(E[] arr, int l, int r) {
  12.         if (l >= r) {
  13.             return;
  14.         }
  15.         //生成一个[l,r]间的随机索引
  16.         int randomIndex = random.nextInt(r - l + 1) + l;
  17.         swap(arr, l, randomIndex);
  19.         // arr[l+1,lt]<v, arr[lt+1,i-1]==v, arr[gt,r]>v
  20.         int lt = l;
  21.         int i=l+1;
  22.         int gt = r+1;
  23.         while (i<gt){
  24.             if (arr[i].compareTo(arr[l])<0){
  25.                 lt++;
  26.                 swap(arr, i, lt);
  27.                 i++;
  28.             }else if (arr[i].compareTo(arr[l])>0){
  29.                 gt--;
  30.                 swap(arr, i, gt);
  31.             }else {
  32.                 i++;
  33.             }
  34.         }
  35.         swap(arr, l, lt);
  36.         sort(arr, l, lt-1);
  37.         sort(arr, gt, r);
  39.     }
  41.     private static <E extends Comparable<E>> void swap(E[] arr, int i, int j) {
  42.         E temp = arr[i];
  43.         arr[i] = arr[j];
  44.         arr[j] = temp;
  45.     }
  46. }

堆排序

先实现一个最大堆

  1. /**
  2.  * 基于数组实现的最大堆
  3.  */
  4. public class MaxHeap<E extends Comparable<E>> {
  6.     private Array<E> data;
  8.     public MaxHeap(int capacity){
  9.          data = new Array<>(capacity);
  10.     }
  12.     public MaxHeap(){
  13.         data = new Array<>();
  14.     }
  16.     /**
  17.      * 返回堆中元素的个数
  18.      */
  19.     public int size(){
  20.         return data.getSize();
  21.     }
  23.     /**
  24.      * 堆是否为空
  25.      */
  26.     public boolean isEmpty(){
  27.         return data.isEmpty();
  28.     }
  30.     /**
  31.      * 返回索引处元素的父节点的索引
  32.      */
  33.     private int parent(int index){
  34.         if (index == 0){
  35.             throw new IllegalArgumentException("根节点没有父节点");
  36.         }
  37.         return (index-1)/2;
  38.     }
  40.     /**
  41.      * 返回索引处元素的左孩子的索引
  42.      */
  43.     private int leftChild(int index){
  44.         return index*2+1;
  45.     }
  47.     /**
  48.      * 返回索引处元素的右孩子的索引
  49.      */
  50.     private int rightChild(int index){
  51.         return (index+1)*2;
  52.     }
  54.     /**
  55.      * 交换元素
  56.      */
  57.     private void swap(int i, int j){
  58.         E temp = data.get(i);
  59.         data.set(i, data.get(j));
  60.         data.set(j, temp);
  61.     }
  63.     /**
  64.      * 向堆中插入元素
  65.      */
  66.     public void add(E e){
  67.         data.addLast(e);
  68.         //进行堆的上浮
  69.         int size = data.getSize();
  70.         if (size >1){
  71.             int index = size -1;
  72.             while (index >0 && e.compareTo(data.get(parent(index))) > 0){
  73.                 swap(index, parent(index));
  74.                 index = parent(index);
  75.             }
  76.         }
  77.     }
  79.     /**
  80.      * 返回堆中最大元素
  81.      */
  82.     public E findMax(){
  83.         if (data.isEmpty()){
  84.             throw new IllegalArgumentException("当前堆为空");
  85.         }
  86.         return data.get(0);
  87.     }
  89.     /**
  90.      * 取出堆中的最大元素
  91.      */
  92.     public E extractMax(){
  93.         E ret = findMax();
  94.         swap(0, data.getSize()-1);
  95.         data.removeLast();
  96.         siftDown(0);
  97.         return ret;
  98.     }
  100.     /**
  101.      * 下沉操作
  102.      */
  103.     private void siftDown(int k){
  104.         while (leftChild(k) < data.getSize()){
  105.             int j = leftChild(k);
  106.             //data[j]是leftChild和rightChild中的最大值
  107.             if ((j+1)<data.getSize() && data.get(j+1).compareTo(data.get(j))>0){
  108.                 j = rightChild(k);
  109.             }
  110.             if (data.get(k).compareTo(data.get(j))>=0){
  111.                 break;
  112.             }
  113.             //如果data[k]比data[j]小，则继续下沉
  114.             swap(k, j);
  115.             k = j;
  116.         }
  117.     }
  119.     @Override
  120.     public String toString(){
  121.         StringBuilder stringBuilder = new StringBuilder();
  122.         for (int i=0;i<data.getSize();i++){
  123.             stringBuilder.append(data.get(i)).append(" ");
  124.         }
  125.         return stringBuilder.toString();
  126.     }
  128. }
  1. 然后进行堆排序
  1. /**
  2.  * 堆排序
  3.  */
  4. public class HeapSort {
  6.     private HeapSort(){}
  8.     public static <E extends Comparable<E>> void sort(E[] data){
  9.         MaxHeap<E> maxHeap = new MaxHeap<>();
  10.         for (E e : data) {
  11.             maxHeap.add(e);
  12.         }
  13.         for (int i=0;i<data.length;i++){
  14.             data[data.length-i-1] = maxHeap.extractMax();
  15.         }
  16.     }
  17. }

此外，堆还有heapify方法，该方法可以将任意数组转化为堆。以堆的构造方法写出

  1. public MaxHeap(E[] arr) {
  2.     data = new Array<>();
  3.     for (E e : arr) {
  4.         data.addLast(e);
  5.     }
  6.     //从最后一个非叶子节点开始进行下沉操作
  7.     for (int i = parent(arr.length - 1); i >= 0; i--) {
  8.         siftDown(i);
  9.     }
  10. }

堆的replace方法

  1. /**
  2.  * 取出堆中最大元素，并且替换成元素e
  3.  */
  4. public E replace(E e) {
  5.     E ret = findMax();
  6.     data.set(0, e);
  7.     siftDown(0);
  8.     return ret;
  9. }

上述的堆排序算法创建了额外的空间，现在对上述的堆排序算法进行改进，进行原地堆排序算法

  1. public static <E extends Comparable<E>> void siteSort(E[] data) {
  2.     if (data.length == 1) {
  3.         return;
  4.     }
  5.     for (int i = data.length / 2 - 1; i >= 0; i--) {
  6.         siftDown(data, i, data.length);
  7.     }
  8.     for (int i=data.length-1;i>=0;i--){
  9.         swap(data,0,i);
  10.         siftDown(data,0,i);
  11.     }
  12. }
  14. /**
  15.  * 对data[0,n)所形成的最大堆中，索引k的元素，执行siftDown下沉操作
  16.  */
  17. private static <E extends Comparable<E>> void siftDown(E[] data, int k, int n) {
  18.     while (2 * k + 1 < n) {
  19.         int j = 2 * k + 1;
  20.         //data[j]是leftChild和rightChild中的最大值
  21.         if ((j + 1) < n && data[j + 1].compareTo(data[j]) > 0) {
  22.             j = 2 * k + 2;
  23.         }
  24.         if (data[k].compareTo(data[j]) >= 0) {
  25.             break;
  26.         }
  27.         //如果data[k]比data[j]小，则继续下沉
  28.         swap(data, k, j);
  29.         k = j;
  30.     }
  31. }
  33. private static <E extends Comparable<E>> void swap(E[] data, int i, int j) {
  34.     E temp = data[i];
  35.     data[i] = data[j];
  36.     data[j] = temp;
  37. }