• Divide & Conquer + Optimal substructure 分治 + 最有子结构

    1. 斐波那契饿数列

  • 递归 指数 O(2^n)

    1.   public int fib(int n) {
    2.       if (n <= 1) {
    3.           return n;
    4.       }
    6.       return fib(n-1) + fib(n-2);
    7.   }

  • 缓存

    1.   public int fib(int n, int[] memo) {
    2.       if (n <= 1) {
    3.           return n;
    4.       }
    5.       if (memo[n] == 0){
    6.           memo[n] = fib(n-1) + fib(n-2);
    7.       }
    9.       return memo[n];
    10.   }

  • 循环

    1.   public int fib(int n) {
    2.       if (n <= 3) {
    3.           return n;
    4.       }
    5.       int a = 1, b = 2, c = 3;
    6.       for (int i = 0; i < n - 3; i++) {
    7.           a = b;
    8.           b = c;
    9.           c = a + b;
    10.       }
    12.       return c;
    13.   }

    2. 最长有效括号 32

3. 跳跃游戏1 55

4. 跳跃游戏2 45

5. 最大子数组和 53

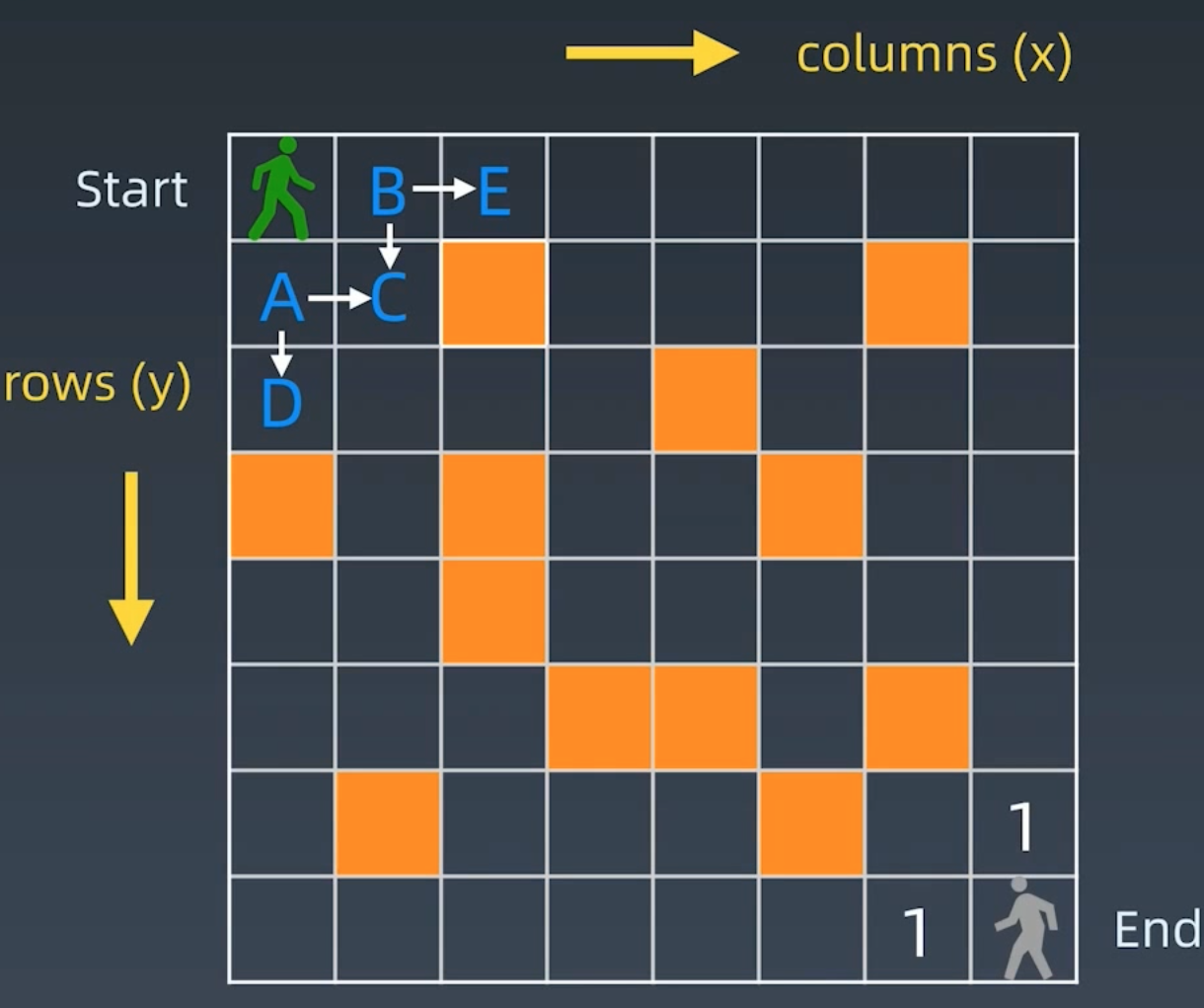
6. 不同路径 62

7. 不同路径2 63

8. 最小路径和 64

9. 爬楼梯 70

10. 编辑距离 72

11. 最小覆盖子串 76

12. 三角形最小路径和

13. 买卖股票的最佳时机

14. 买卖股票的最佳时机 II

15. 买卖股票的最佳时机 III

16. 乘积最大子数组

17. 买卖股票的最佳时机 IV

18. 打家劫舍

19. 打家劫舍 II

20. 最大正方形

21. 完全平方数

22. 最佳买卖股票时机含冷冻期

23. 戳气球

24. 零钱兑换

25. 矩形区域不超过 K 的最大数值和

26. 青蛙过河

27. 分割数组的最大值

28. 零钱兑换 II

29. 学生出勤记录 II

30. 任务调度器

31. 回文子串

32. 买卖股票的最佳时机含手续费

33. 不同路径 III

34. 最长公共子序列

35. 路径的数目

image.png

  • 递归

    1.   public int countPaths(boolean[][] grid, int row, int col){
    2.        if (!validSquare(grid, row, col)){
    3.           return 0;
    4.       }
    5.       if (isEnd(grid, row, col)) {
    6.           return 1;
    7.       }
    8.       return countPaths(grid, row + 1, col) + countPath(grid, row, col + 1);
    9.   }

  • dp数组

    36. 解码方法 91