基本思想

每步将一个待排序的记录，按其顺序码大小插入到前面已经排序的字序列的合适位置（从后向前找到合适位置后），直到全部插入排序完为止。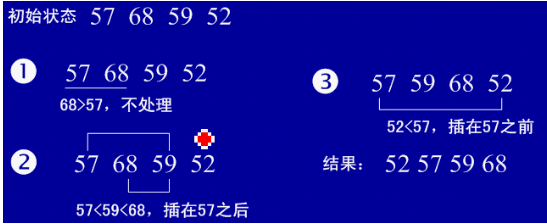
直接插入排序 - 图1

代码实现

  1. public class DirectInsertionSort {
  3.     public static void main(String[] args) {
  4.         int[] a={49,38,65,97,76,13,27,49,78,34,12,64,1};
  5.         System.out.println("排序之前：");
  6.         for (int i = 0; i < a.length; i++) {
  7.             System.out.print(a[i]+" ");
  8.         }
  9.         //直接插入排序
  10.         for (int i = 1; i < a.length; i++) {
  11.             //待插入元素
  12.             int temp = a[i];
  13.             int j;
  14.             /*for (j = i-1; j>=0 && a[j]>temp; j--) {
  15.                 //将大于temp的往后移动一位
  16.                 a[j+1] = a[j];
  17.             }*/
  18.             for (j = i-1; j>=0; j--) {
  19.                 //将大于temp的往后移动一位
  20.                 if(a[j]>temp){
  21.                     a[j+1] = a[j];
  22.                 }else{
  23.                     break;
  24.                 }
  25.             }
  26.             a[j+1] = temp;
  27.         }
  28.         System.out.println();
  29.         System.out.println("排序之后：");
  30.         for (int i = 0; i < a.length; i++) {
  31.             System.out.print(a[i]+" ");
  32.         }
  33.     }
  34. }
  1. /**  
  2.  * 插入排序<br/>  
  3.  * <ul>  
  4.  * <li>从第一个元素开始，该元素可以认为已经被排序</li>  
  5.  * <li>取出下一个元素，在已经排序的元素序列中从后向前扫描</li>  
  6.  * <li>如果该元素（已排序）大于新元素，将该元素移到下一位置</li>  
  7.  * <li>重复步骤3，直到找到已排序的元素小于或者等于新元素的位置</li>  
  8.  * <li>将新元素插入到该位置中</li>  
  9.  * <li>重复步骤2</li>  
  10.  * </ul>  
  11.  * @param numbers  
  12.  */  
  13. public static void insertSort(int[] numbers) {   
  14.     int size = numbers.length, temp, j;   
  15.     for(int i=1; i<size; i++) {   
  16.         temp = numbers[i];   
  17.         for(j = i; j > 0 && temp < numbers[j-1]; j--)   
  18.             numbers[j] = numbers[j-1];   
  19.         numbers[j] = temp;   
  20.     }   
  21. }
  1. public class InsertionSort<T extends Comparable<T>> {
  3.     private InsertionSort() { }
  5.     public static <T extends Comparable<T>> T[] sort(T[] unsorted) {
  6.         int length = unsorted.length;
  7.         for (int i = 1; i < length; i++) {
  8.             sort(i, unsorted);
  9.         }
  10.         return unsorted;
  11.     }
  13.     private static <T extends Comparable<T>> void sort(int i, T[] unsorted) {
  14.         for (int j = i; j > 0; j--) {
  15.             T jthElement = unsorted[j];
  16.             T jMinusOneElement = unsorted[j - 1];
  17.             if (jthElement.compareTo(jMinusOneElement) < 0) {
  18.                 unsorted[j - 1] = jthElement;
  19.                 unsorted[j] = jMinusOneElement;
  20.             } else {
  21.                 break;
  22.             }
  23.         }
  24.     }
  25. }

总结

  1. 直接插入排序是稳定的排序。关于各种算法的稳定性分析可以参考 常用排序算法稳定性分析
  3. 文件初态不同时，直接插入排序所耗费的时间有很大差异。若文件初态为正序，则每个待插入的记录只需要比较一次就能够找到合适的位置插入，故算法的时间复杂度为O(n)，这时最好的情况。若初态为反序，则第i个待插入记录需要比较i+1次才能找到合适位置插入，故时间复杂度为O(n2)，这时最坏的情况。
  5. 直接插入排序的平均时间复杂度为O(n^2)。