43字符串相乘

题目链接

题目描述：

给定两个以字符串形式表示的非负整数 num1 和 num2，返回 num1 和 num2 的乘积，它们的乘积也表示为字符串形式。

示例 1:

输入: num1 = “2”, num2 = “3”
输出: “6”

示例 2:

输入: num1 = “123”, num2 = “456”
输出: “56088”

说明：

num1 和 num2 的长度小于110。
num1 和 num2 只包含数字 0-9。
num1 和 num2 均不以零开头，除非是数字 0 本身。
不能使用任何标准库的大数类型（比如 BigInteger）或直接将输入转换为整数来处理。

解题思路

  本题难点在于如何复原我们日常的思维方式，也就是从小就会的竖式相乘法。这里仅提供一个暴力法，上图～

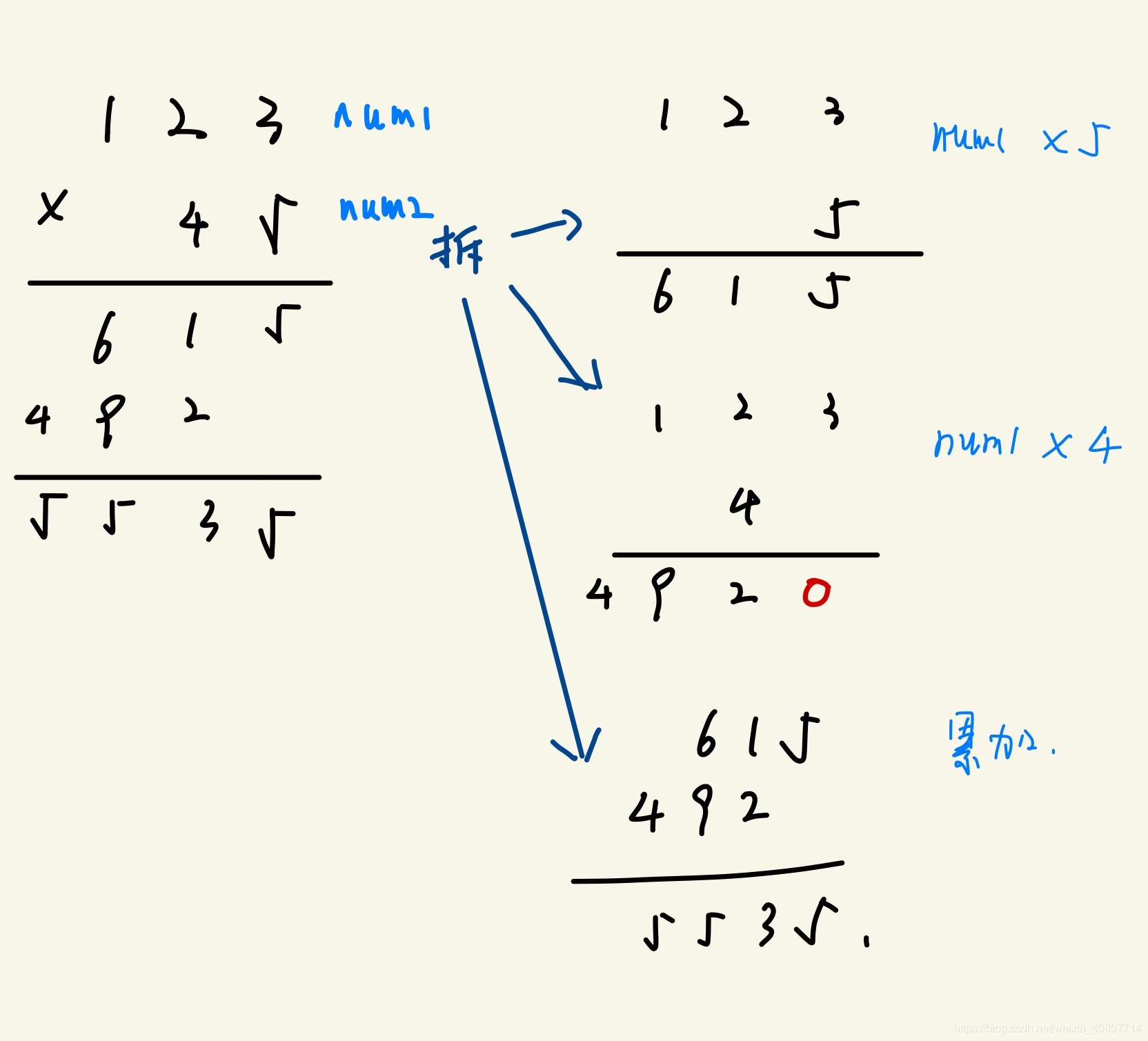
  由图可知，实际上就是遍历num2数字，使之与num1相乘，最后将结果累加。
  在逐项相乘部分，要考虑一个问题——补0。而包括逐项相乘和逐项累加都是#415.字符串相加的延续，题解在此～
  简单来说，无论乘法还是加法都要考虑三个问题：

1. 进位问题，carry = (n1 * n2 + carry) / 10和carry = (n1 + n2 + carry) / 10均表示当前位相乘或相加后的进位结果；
2. 最高位溢出问题，这里包含两部分。是如果最高位计算完成后也发生了进位情况应该怎么办？可以在for循环中添加carry != 0，那么这就会引发第二个问题，如果i或j已经遍历完毕了怎么办？这时可以用一个三目运算符解决问题n1 = j < 0 ? 0 : num1[j] - '0'；
3. 当前位计算问题，当然是product = (n1 * n2 + carry) % 10并将结果添加到temp末尾

  另外要注意，循环结束后结果是倒叙的，需要先reverse以下再进行计算～

代码

class Solution {
public:
    string multiply(string num1, string num2) {
        if(num1 == "0" || num2 == "0")
            return "0";
        string result = "";
        for(int i = num2.size() - 1; i >= 0; i--){
            int carry = 0;
            string temp = "";
            //补0
            for(int j = 0; j < num2.size() - 1 - i; j++){
                temp += '0';
            }
            int n2 = num2[i] - '0';
            for(int j = num1.size() - 1; j >= 0 || carry != 0; j--){
                int n1 = j < 0 ? 0 : num1[j] - '0';
                int product = (n1 * n2 + carry) % 10;
                temp += to_string(product);
                carry = (n1 * n2 + carry) / 10;
            }
            reverse(temp.begin(), temp.end());
            result = addString(result, temp);
        }
        return result;
    }
    string addString(string num1, string num2){
        string result = "";
        int carry = 0;
        for(int i = num1.size() - 1, j = num2.size() - 1; i >= 0 || j >= 0 || carry != 0; i--, j--){
            int n1 = i < 0 ? 0 : num1[i] - '0';
            int n2 = j < 0 ? 0 : num2[j] - '0';
            int temp = (n1 + n2 + carry) % 10;
            result += to_string(temp);
            carry = (n1 + n2 + carry) / 10;
        }
        reverse(result.begin(), result.end());
        return result;
    }
};

如果有错误或者不严谨的地方，请务必给予指正，十分感谢。